This year was my first time participating in the FCSC. I decided to focus on reverse engineering challenges. I managed to solve 7 out of the 8 challenges, which I’m quite happy about! The challenges were all varied and very interesting, so I want to thank all the authors for this :)
babyfuscation
Un reverse (très) légèrement obfusqué !
Solves: 379
Difficulty: ⭐
In this challenge, we are given a standard x64 ELF executable that prompts for an input:
$ ./babyfuscation
Enter the flag:
test
Wrong flag. Try again!
After loading the binary into IDA, here’s what we see:
int __fastcall main(int argc, const char **argv, const char **envp)
{
int i; // [rsp+4h] [rbp-Ch]
int j; // [rsp+8h] [rbp-8h]
int k; // [rsp+Ch] [rbp-4h]
for ( i = 0; i <= 79; ++i )
{
envp = (const char **)VYeXkgjLLMrczyw7i7dJPkyAbxqgCahe;
VYeXkgjLLMrczyw7i7dJPkyAbxqgCahe[i] ^= 0x42u;
}
for ( j = 0; j <= 79; ++j )
{
envp = (const char **)a93rEUcvwf4Ec9KHKqzFx7wL;
a93rEUcvwf4Ec9KHKqzFx7wL[j] ^= 0x13u;
}
for ( k = 0; k <= 79; ++k )
{
envp = (const char **)ouPrjEhgqPVNXCqchuzw7WTWLHnkbwqj;
ouPrjEhgqPVNXCqchuzw7WTWLHnkbwqj[k] ^= 0x37u;
}
VsvYbpipYYgRoCeFtoxhtAmdFuNu3WvV(argc, argv, envp);
wKtyPoT4WdyrkVzhvYUfvqo3M9iPVMd3();
return VakkEeHbtHMpNqXPMkadR4v7K();
}
The function names as well as the constants are obfuscated. It also appears that some constants are deobfuscated at runtime. After manually deobfuscating it, we get:
int __fastcall main(int argc, const char **argv, const char **envp)
{
int i; // [rsp+4h] [rbp-Ch]
int j; // [rsp+8h] [rbp-8h]
int k; // [rsp+Ch] [rbp-4h]
for ( i = 0; i <= 79; ++i )
enter_flag_str[i] ^= 0x42u;
for ( j = 0; j <= 79; ++j )
correct_flag_str[j] ^= 0x13u;
for ( k = 0; k <= 79; ++k )
wrong_flag_str[k] ^= 0x37u;
get_user_input();
scramble_user_input();
return check_user_input(argc, argv);
}
The function get_user_input() reads 80 characters from stdin and stores them in the BSS section. Then, scramble_user_input() scrambles the input as follows:
__int64 scramble_flag()
{
__int64 result; // rax
int i; // [rsp+8h] [rbp-8h]
int v2; // [rsp+Ch] [rbp-4h]
v2 = strlen(user_input) + 1;
for ( i = 0; i < v2; ++i )
scrambled_input[i] = ((user_input[i] >> 5) | (8 * user_input[i])) ^ (3 * i + 31);
result = v2;
scrambled_input[v2] = 0;
return result;
}
Finally, check_user_input() checks if the scrambled user input matches a hardcoded byte array, and displays a success or failure message accordingly:
__int64 check_user_input()
{
if ( (unsigned int)are_bytearray_equal(scrambled_input, &scrambled_flag) )
{
puts(correct_flag_str);
return 0LL;
}
else
{
puts(wrong_flag_str);
return 1LL;
}
}
The scrambling process can be easily inverted with the following Python script:
scrambled_flag = bytes.fromhex(
"2D38BF32F005A8B5049B8C53CAE7F067F659C4F150E77AA574ABDCD950F75ABDB62B9E319037" \
"081D3EA92C690A67389F0E2B2493721F406DD47BEE511A4FCA6DECF124CB7205F1"
)
flag = []
for i, c in enumerate(scrambled_flag):
x = c ^ (3 * i + 31)
flag.append(((x & 0b111) << 5) | (x >> 3))
print(bytes(flag))
Flag: FCSC{e30f46b147e7a25a7c8b865d0d895c7c7315f69582f432e9405b6d093b6fb8d3}
Hit or MIPS
Saurez-vous trouver l’entrée menant au succès ?
Solves: 86
Difficulty: ⭐
In this challenge, we are given a MIPS32 ELF binary. For some unknown reason, qemu-mips segfaults when trying to run the binary, so we will solve it statically. Here’s what the main function looks like after some renaming:
int __fastcall main(int argc, char **argv, char **envp)
{
int return_code; // $s1
int k; // $s7
_BYTE *i; // $fp
char v6; // $at
char byte_value; // $v0
bool v8; // dc
int i1; // $v1
_DWORD *modified_byte_array; // $v0
char *v11; // $at
_BYTE *v12; // $a2
int j; // $v1
int *v14; // $at
_DWORD *v15; // $a2
int valid_ints; // $v1
char *end_ptr; // [sp+10h] [-68h] BYREF
_BYTE parsed_byte_array[32]; // [sp+14h] [-64h] BYREF
char hex_nibbles[2]; // [sp+34h] [-44h] BYREF
char v21; // [sp+36h] [-42h] BYREF
_BYTE input[64]; // [sp+38h] [-40h] BYREF
memset(input, 0, sizeof(input));
v21 = 0;
printf("Input? ");
return_code = 1;
if ( fread(input, 1u, 5u, stdin) == 5 && !bcmp("FCSC{", input, 5u) )
{
return_code = 1;
if ( fread(input, 1u, 64u, stdin) == 64 )
{
k = 0;
for ( i = parsed_byte_array; ; ++i )
{
v6 = input[k + 62];
hex_nibbles[0] = input[k + 63];
hex_nibbles[1] = v6;
byte_value = _strtol_internal(hex_nibbles, &end_ptr, 16, 0);
v8 = end_ptr != &v21;
*i = byte_value;
if ( v8 )
break;
k -= 2;
if ( k == -64 )
{
return_code = 1;
if ( fread(input, 1u, 1u, stdin) == 1 && input[0] == '}' )
{
i1 = 0;
modified_byte_array = parsed_byte_array;
do
{
v11 = &xor_constants[i1];
v12 = &parsed_byte_array[i1++];
*v12 ^= *v11;
}
while ( i1 != 32 );
for ( j = 0; j != 8; ++j )
{
v14 = &add_constants[j];
v15 = &parsed_byte_array[j * 4];
*v15 += *v14 + __CFADD__(*v15, *v14);
}
valid_ints = 0;
while ( *modified_byte_array == final_integers[valid_ints ^ 7] )
{
++valid_ints;
++modified_byte_array;
if ( valid_ints == 8 )
{
puts("Success!");
return 0;
}
}
return 2;
}
return return_code;
}
}
}
}
return return_code;
}
In summary, the main function does the following:
- Reads 70 bytes of input, verifies that the first five characters are
FCSC{and that the last character is}. - Parses the 64 characters between the braces as a 32-byte hexadecimal string, starting from the end and mirrored. This means a string like
abcdwould be parsed asparsed_byte_array = [0xdc, 0xba]. - XORs each of the 32 bytes with hardcoded constants.
- Interprets the modified byte array as an array of 8 integers, and adds constants to each integer.
- Finally, verifies that the 8 integers match hardcoded expected integers.
All of these operations can be easily inverted to recover the correct input:
def unpack_int_array(hexstr):
byte_array = bytes.fromhex(hexstr)
return [
int.from_bytes(byte_array[i : i + 4], "big")
for i in range(0, len(byte_array), 4)
]
final_integers = unpack_int_array(
"464353437B3575386D31375F376831352D346E647E31303035333D683472647D"
)
add_constants = unpack_int_array(
"14BC2D8AA9535C19970D4BC7DC9277A63067A42E224E7C1E760E8367E781FA45"
)
xor_constants = unpack_int_array(
"7D2CB4E6A6535C7E61F4D2C94C6B11A53F91ADB4BBD81C7419F8E39981E70ADD"
)
input_integers = []
for i in range(8):
input_integers.append(final_integers[i ^ 7])
# Reverse the add operation
for i, add_cst in enumerate(add_constants):
input_integers[i] = (input_integers[i] - add_cst) & 0xFFFFFFFF
# Reverse the xor operation
for i, xor_cst in enumerate(xor_constants):
input_integers[i] ^= xor_cst
# Mirror everything
flag = b"".join([x.to_bytes(4, "big") for x in input_integers])
print("FCSC{" + flag.hex()[::-1] + "}")
Flag:FCSC{022562fd8421edc1537aa31f3b021983817eacc11a637d6803dbc8d25128a926}
Chatouille
Solves: 11
Difficulty: ⭐⭐
Once again, we are given an x64 ELF binary that checks a user input. Here’s what the main function looks like after a bit of renaming:
__int64 __fastcall main(int argc, char **argv, char **envp)
{
int input_length; // eax
int trimmed_input_length; // edx
int newline_index; // eax
_WORD user_input[68]; // [rsp+0h] [rbp-88h] BYREF
memset(user_input, 0, 128uLL);
input_length = read(0, user_input, 128uLL);
if ( input_length <= 0 )
{
perror("read");
exit(1);
}
trimmed_input_length = input_length;
newline_index = input_length - 1;
if ( *((_BYTE *)user_input + newline_index) == '\n' )
{
*((_BYTE *)user_input + newline_index) = 0;
trimmed_input_length = newline_index;
}
if ( trimmed_input_length != 118
|| (LOBYTE(user_input[59]) = 0x80, user_input[63] = 0xB003, !check1((__int64)user_input))
|| !check2((__int64)user_input) )
{
puts(":(");
exit(0);
}
puts("\\o/");
return 0LL;
}
The main function does the following:
- Reads 128 characters from stdin and removes the newline if present.
- Verifies that the input length is 118 and appends the following 10 bytes:
0x80 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x03 0xB0, producing a 128-byte array. - Checks that both
check1andcheck2return True when given this buffer.
After a quick analysis, check1 seems to hash the input buffer and compare it to a hardcoded hash. The hashing algorithm is most likely SHA-256 (or a slightly modified version), given the use of SIMD instructions like sha256rnds2 and sha256msg1, and constants that match SHA-256 constants when googled. However, we won’t bother reversing it since it’s pretty unlikely that we can invert a hash function. Let’s focus on the second check instead!
Inverting the main check function
Opening check2 in IDA, we get:
_BOOL8 __fastcall main_check(__int64 _RDI)
{
__asm
{
vmovdqu xmm6, xmmword ptr [rdi]
vmovdqu xmm0, xmmword ptr [rdi+10h]
vmovdqu xmm10, xmmword ptr [rdi+20h]
vpshufd xmm1, xmm6, 39h ; '9'
sha256msg1 xmm0, xmm6
vpshufd xmm2, xmm1, 39h ; '9'
sha256msg1 xmm0, xmm1
vpshufd xmm3, xmm2, 39h ; '9'
sha256msg1 xmm0, xmm2
vmovdqu xmm2, xmmword ptr [rdi+30h]
vpshufd xmm4, xmm3, 39h ; '9'
sha256msg1 xmm0, xmm3
vpshufd xmm5, xmm4, 39h ; '9'
... ; Approximately 4000 more SIMD instructions
vpshufd xmm13, xmm4, 39h ; '9'
sha256msg1 xmm7, xmm4
vpshufd xmm12, xmm13, 39h ; '9'
sha256msg1 xmm7, xmm13
vpxor xmm8, xmm12, cs:hardcoded_cst7
vpxor xmm7, xmm7, cs:hardcoded_cst8
vpxor xmm12, xmm12, xmm12
vpor xmm14, xmm11, xmm8
vpor xmm4, xmm5, xmm7
vpor xmm13, xmm14, xmm4
vpcmpeqd xmm0, xmm13, xmm12
vpmovmskb eax, xmm0
}
return _EAX == 0xFFFF;
}
Alright, we’re facing a crazy amount of SIMD instructions. It looks like the input buffer is split into 8 chunks of 16 bytes each, stored in XMM registers using instructions like vmovdqu xmm6, xmmword ptr [rdi]. After that, the chunks are modified using vpshufd and sha256msg1 SIMD instructions.
After modification, each chunk is compared to a hardcoded constant using vpxor. The results are ORed together, and the final result is stored in xmm13. Finally, using vpcmpeqd and vpmovmskb, eax is set.
Understanding what’s going on
Our goal is to have eax == 0xFFFF. A quick search shows that this happens if xmm13 == xmm12 during vpcmpeqd xmm0, xmm13, xmm12. Since xmm12 is set to zero just before, we want xmm13 == 0, meaning all the modified chunks must match the constants they’re XORed against.
In “pseudo-Python”, check2 looks like:
def check2(input_buffer):
is_input_valid = True
modified_chunks = modify_chunks(input_buffer)
is_input_valid &= modified_chunks[0] == hardcoded_cst1
is_input_valid &= modified_chunks[1] == hardcoded_cst2
is_input_valid &= modified_chunks[2] == hardcoded_cst3
is_input_valid &= modified_chunks[3] == hardcoded_cst4
is_input_valid &= modified_chunks[4] == hardcoded_cst5
is_input_valid &= modified_chunks[5] == hardcoded_cst6
is_input_valid &= modified_chunks[6] == hardcoded_cst7
is_input_valid &= modified_chunks[7] == hardcoded_cst8
return is_input_valid
Note: in this pseudo-code modify_chunks is a function that modify each chunks based on a sequence of vpshufd and sha256msg1 operations
Now let’s look at what vpshufd and sha256msg1 instructions does.
vpshufd
vpshufd dst, src, imm8
This instruction shuffles the 32-bit words (doublewords) inside a 128-bit source register according to imm8 and store the result in a destination register.
The two low bits of
imm8indicates which doubleword ofsrcwill be the lower doubleword ofdst.Then the fourth and third bits of
imm8indicates which doubleword ofsrcwill be the second doubleword ofdstand so on…
In our case imm8 is always equal to 0x39 whose binary representation is 00 11 10 01. So if we denotes src as src=[dw4, dw3, dw2, dw1] we have:
dst[0] = src[0b01] = src[1]
dst[1] = src[0b10] = src[2]
dst[2] = src[0b11] = src[3]
dst[3] = src[0b01] = src[0]
This mean in our case, because it is always used with the immediate 0x39, vpshufd boils down to a simple 32-bits rotate right.
sha256msg1
sha256msg1 xmm1, xmm2
This instruction is a bit more complex, if we consider xmm1 and xmm2 as registers of four doublwords then this instruction does:
xmm1[0] = xmm1[0] + sigma0(xmm1[1])
xmm1[1] = xmm1[1] + sigma0(xmm1[2])
xmm1[2] = xmm1[2] + sigma0(xmm1[3])
xmm1[3] = xmm1[3] + sigma0(xmm2[0])
Where
def sigma0(x):
return RotateRight(x, 7) ^ RotateRight(x, 18) ^ (x >> 3)
Putting it all together
Now that we undestand how the two instructions transform the input chunks, we can reimplement this check2 function in Python and solve for the input that gives xmm13 == 0 using the Z3 solver. Here is the final script. It basically parse the check2 instructions from the IDA output, apply the function to symbolic BitVec variables that represent each chunks of the input and solve for xmm13 == 0.
from z3 import *
from parsing_func import *
def sigma0(x):
return RotateRight(x, 7) ^ RotateRight(x, 18) ^ LShR(x, 3)
def z3_get_nth_word(x, n):
return Extract(n * 32 + 31, n * 32, x)
def z3_sha256msg1(x0, x1):
# x0 and x1 are two 128 bit BitVec
w0 = z3_get_nth_word(x0, 0)
w1 = z3_get_nth_word(x0, 1)
w2 = z3_get_nth_word(x0, 2)
w3 = z3_get_nth_word(x0, 3)
w4 = z3_get_nth_word(x1, 0)
# w0, w1, w2, w3, w4 are 32 bits BitVec
z0 = w0 + sigma0(w1)
z1 = w1 + sigma0(w2)
z2 = w2 + sigma0(w3)
z3 = w3 + sigma0(w4)
# z0, z1, z2, z3 are 32s bit BitVec
z0e = ZeroExt(96, z0)
z1e = ZeroExt(96, z1)
z2e = ZeroExt(96, z2)
z3e = ZeroExt(96, z3)
# z0e, z1e, z2e, z3e are 128 bits BitVec
return z0e | (z1e << 32) | (z2e << 64) | (z3e << 96)
csts = {
"xmmword_9040": 0x0BD7A8C92FE4A7BD964145C1B415E27FE,
"xmmword_9050": 0x4FB98600728660ADC7EB49ABF5F4BB97,
"xmmword_9060": 0x36DE1DABA4D0C410A59ABC08D9270088,
"xmmword_9070": 0x0B6CEB5305C48B5C137C1EEC542DD7AB5,
"xmmword_9080": 0x4325F6DFDC17B3D93A437A2FD174192F,
"xmmword_9090": 0x67172D37B77DAEFE99DB1D1FF04FBED5,
"xmmword_90A0": 0x0AB509EB2143D13035F595D84BF7A1DBF,
"xmmword_90B0": 0x27E2993E7DDB9BCE388260CED6DF027E,
}
# XMM registers
xmms = [None for _ in range(16)]
with open("check2_insns.txt", "r") as f:
# ignore the last two simd instruction used for equality check
lines = [l.strip() for l in f.readlines()][:-2]
# Our 8 chunks of 16 bytes each
input_blocks = [BitVec(f"b{i}", 16 * 8) for i in range(8)]
for insn in lines:
mnem = insn.split()[0]
if mnem == "vmovdqu":
dst, offset = parse_vmovdqu(insn)
xmms[dst] = input_blocks[offset // 16]
elif mnem == "vpor":
dst, op1, op2 = parse_simd_binary_op(insn)
xmms[dst] = xmms[op1] | xmms[op2]
elif mnem == "vpxor":
dst, op1, op2 = parse_vpxor(insn)
if type(op2) == str:
xmms[dst] = xmms[op1] ^ csts[op2]
else:
xmms[dst] = xmms[op1] ^ xmms[op2]
elif mnem == "vpshufd":
dst, src, imm8 = parse_vpshufd(insn)
xmms[dst] = RotateRight(xmms[src], 32)
elif mnem == "sha256msg1":
dst, src = parse_sha256msg1(insn)
xmms[dst] = z3_sha256msg1(xmms[dst], xmms[src])
else:
raise ValueError("Unexpected instruction", insn)
s = Solver()
s.add(xmms[13] == 0)
# Ensure the solution start with 'FCSC{'
s.add(
Extract(39, 0, input_blocks[0])
== BitVecVal(int.from_bytes(b"FCSC{", "little"), 5 * 8)
)
# Ensure the solution end with '}' and 80 00 00 00 00 00 00 00 03 B0
s.add(
Extract(127, 40, input_blocks[7])
== BitVecVal(0xB00300000000000000807D, 11 * 8)
)
print("[*] Solving")
r = s.check()
if r == sat:
m = s.model()
flag = b""
for b in input_blocks:
flag += m[b].as_long().to_bytes(16, "little")
print(flag[0:118].decode())
else:
print(r)
print("No solutions :(")
Note: Parsing functions code is omitted for brevity; they are based on simple regex matching.
After around 25 minutes of solving…
Flag:FCSC{Shoh4IeFohmee1oichoo5iujohze2riPuuroochoh3vi0aGai5ae5aithooph2wohquai2takaeng9eeF3ue8QuooT2shiege5ee5ahL1vanoAnZ}
Coloratops
Voici un crackme plein de couleurs avec des allures old school.
Solves: 50
Difficulty: ⭐⭐
In this challenge, we are given an x64 ELF binary using the SDL library. When running the game, here’s what we see:
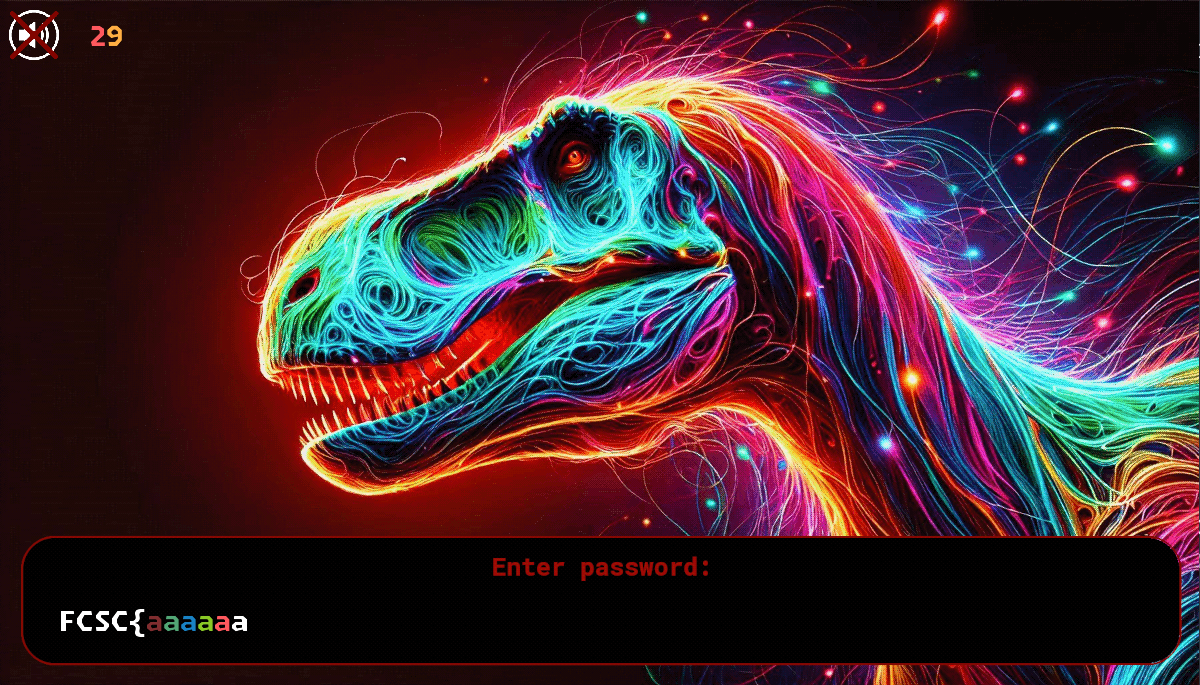
The first thing to notice is that the input charset is restricted to FCSC{}abcdef0123456789, and the colors of the input characters change based on what is typed. Here’s what the main function looks like after some renaming:
int __fastcall main(int argc, const char **argv, const char **envp)
{
__int64 v3; // rdx
__int64 v5; // rdi
__int64 v6; // rax
size_t v7; // rax
__int64 v8; // rax
size_t v9; // rax
_BYTE flag_sha256[64]; // [rsp+10h] [rbp-130h] BYREF
_DWORD v11[6]; // [rsp+50h] [rbp-F0h] BYREF
char v12[8]; // [rsp+68h] [rbp-D8h] BYREF
int v13[3]; // [rsp+70h] [rbp-D0h] BYREF
char inp_buf[8]; // [rsp+7Ch] [rbp-C4h] BYREF
int keyPressed; // [rsp+84h] [rbp-BCh]
__int16 ctrKeyFlag; // [rsp+88h] [rbp-B8h]
_DWORD v17[2]; // [rsp+B0h] [rbp-90h] BYREF
int v18; // [rsp+B8h] [rbp-88h]
int v19; // [rsp+BCh] [rbp-84h]
int v20; // [rsp+C0h] [rbp-80h] BYREF
__int16 v21; // [rsp+C4h] [rbp-7Ch]
char v22; // [rsp+C6h] [rbp-7Ah]
__int16 v23; // [rsp+C8h] [rbp-78h]
void *(__fastcall *v24)(__int64, void *, int); // [rsp+D0h] [rbp-70h]
__int64 v25; // [rsp+D8h] [rbp-68h]
char *s; // [rsp+E8h] [rbp-58h]
__int64 v27; // [rsp+F0h] [rbp-50h]
__int64 v28; // [rsp+F8h] [rbp-48h]
unsigned int v29; // [rsp+104h] [rbp-3Ch]
__int64 v30; // [rsp+108h] [rbp-38h]
size_t j; // [rsp+110h] [rbp-30h]
size_t i; // [rsp+118h] [rbp-28h]
int is_game_running; // [rsp+124h] [rbp-1Ch]
__int64 TextureFromSurface; // [rsp+128h] [rbp-18h]
if ( (unsigned int)SDL_Init(32LL, argv, envp) || (int)SDL_Init(17LL, argv, v3) < 0 || (unsigned int)TTF_Init() == -1 )
{
SDL_Quit();
return 1;
}
else
{
sdl_window = SDL_CreateWindow("FCSC 2025 - Coloratops", 805240832LL, 805240832LL, 1200LL, 686LL, 20LL);
if ( sdl_window )
{
render_target = SDL_CreateRenderer(sdl_window, 0xFFFFFFFFLL, 6LL);
if ( render_target )
{
v20 = 48000;
v21 = -32480;
v22 = 2;
v23 = 2048;
v24 = sub_9F01;
v25 = 0LL;
sdl_audiodeviceid = SDL_OpenAudioDevice(0LL, 0LL, &v20, &sdl_audiospec, 11LL);
v5 = render_target;
setup_textures();
SDL_StartTextInput(v5, &font_to_render);
TextureFromSurface = 0LL;
v17[0] = 60;
v17[1] = 600;
v18 = 100;
v19 = 200;
is_game_running = 1;
start_time = SDL_GetTicks();
while ( is_game_running )
{
while ( (unsigned int)SDL_PollEvent(v13) )
{
switch ( v13[0] )
{
case 256:
is_game_running = 0;
break;
case 771:
for ( i = 0LL; ; ++i )
{
v7 = strlen(inp_buf);
if ( i >= v7 )
break;
if ( (unsigned __int64)current_input_length <= 0x3F
&& strchr("FCSC{}abcdef0123456789", inp_buf[i])
&& (unsigned __int64)current_input_length <= 0xFE )
{
v6 = current_input_length++;
user_input[v6] = inp_buf[i];
user_input[current_input_length] = 0;
}
}
break;
case 768:
if ( keyPressed == 8 && (ctrKeyFlag & 0xC0) == 0 && current_input_length )
{
user_input[--current_input_length] = 0;
}
else if ( keyPressed == 113 && (ctrKeyFlag & 0xC0) != 0 )
{
is_game_running = 0;
}
else if ( keyPressed == 99 && (ctrKeyFlag & 0xC0) != 0
|| keyPressed == 8 && (ctrKeyFlag & 0xC0) != 0
|| keyPressed == 27 )
{
memset(user_input, 0, 0x100uLL);
current_input_length = 0LL;
}
else if ( keyPressed == 32 )
{
sound_activated ^= 1u;
SDL_PauseAudioDevice((unsigned int)sdl_audiodeviceid, sound_activated == 0);
}
else if ( keyPressed == 118 && (ctrKeyFlag & 0xC0) != 0 )
{
s = (char *)SDL_GetClipboardText();
if ( s )
{
for ( j = 0LL; ; ++j )
{
v9 = strlen(s);
if ( j >= v9 )
break;
if ( (unsigned __int64)current_input_length <= 0x3F
&& strchr("FCSC{}abcdef0123456789", s[j])
&& (unsigned __int64)current_input_length <= 0xFE )
{
v8 = current_input_length++;
user_input[v8] = s[j];
user_input[current_input_length] = 0;
}
}
SDL_free(s);
}
}
break;
}
}
is_flag_valid = byte_26B264 == '{'
&& byte_26B263 == 'C'
&& byte_26B262 == 'S'
&& byte_26B261 == 'C'
&& user_input[0] == 'F';
LOBYTE(is_flag_valid) = user_input[current_input_length - 1] == '}'
&& byte_26B264 == '{'
&& byte_26B263 == 'C'
&& byte_26B262 == 'S'
&& byte_26B261 == 'C'
&& user_input[0] == 'F';
is_flag_valid = (unsigned __int8)is_flag_valid;
is_flag_valid &= check_flag_validity();
if ( TextureFromSurface )
SDL_DestroyTexture(TextureFromSurface);
if ( !show_end_screen )
{
v30 = TTF_RenderText_Blended(font_to_render, user_input, 0xFFFFFFFFLL);
if ( v30 )
{
TextureFromSurface = SDL_CreateTextureFromSurface(render_target, v30);
v18 = *(_DWORD *)(v30 + 16);
v19 = *(_DWORD *)(v30 + 20);
SDL_FreeSurface(v30);
}
}
SDL_SetRenderDrawColor(render_target, 0LL, 0LL, 0LL, 255LL);
SDL_RenderClear(render_target);
v29 = ((unsigned int)SDL_GetTicks() - start_time) / 1000;
if ( v29 > 59 && !show_end_screen )
show_end_screen = 1;
if ( show_end_screen )
{
SDL_RenderCopy(render_target, end_screen_texture, 0LL, &dst_main_rect);
}
else if ( is_flag_valid )
{
sha256((__int64)user_input, current_input_length, (__int64)flag_sha256);
if ( !flag_texture )
decrypt_texture(render_target, &flag_texture, (__int64)flag_sha256);
SDL_RenderCopy(render_target, flag_texture, 0LL, &dst_main_rect);
}
else
{
SDL_RenderCopy(render_target, main_texture, 0LL, &dst_main_rect);
}
if ( sound_activated )
SDL_RenderCopy(render_target, sound_activated_texture, 0LL, &dst_sounds_rect);
else
SDL_RenderCopy(render_target, sound_deactivated_texture, 0LL, &dst_sounds_rect);
if ( !show_end_screen )
{
snprintf(v12, 8uLL, "%2d ", 60 - v29);
v28 = TTF_RenderText_Blended(font_to_render, v12, 0xFFFFFFFFLL);
if ( !v28 )
break;
v27 = SDL_CreateTextureFromSurface(render_target, v28);
SDL_FreeSurface(v28);
if ( !v27 )
break;
v11[0] = 90;
v11[1] = 15;
v11[2] = *(_DWORD *)(v28 + 16);
v11[3] = *(_DWORD *)(v28 + 20);
SDL_RenderCopy(render_target, v27, 0LL, v11);
SDL_DestroyTexture(v27);
}
if ( TextureFromSurface && !show_end_screen )
SDL_RenderCopy(render_target, TextureFromSurface, 0LL, v17);
SDL_RenderPresent(render_target);
}
SDL_StopTextInput();
if ( main_texture )
SDL_DestroyTexture(main_texture);
if ( flag_texture )
SDL_DestroyTexture(flag_texture);
if ( end_screen_texture )
SDL_DestroyTexture(end_screen_texture);
if ( sound_activated_texture )
SDL_DestroyTexture(sound_activated_texture);
if ( sound_deactivated_texture )
SDL_DestroyTexture(sound_deactivated_texture);
if ( font_to_render )
TTF_CloseFont(font_to_render);
if ( render_target )
SDL_DestroyRenderer(render_target);
if ( sdl_window )
SDL_DestroyWindow(sdl_window);
sub_27C4(qword_26B240);
TTF_Quit();
SDL_Quit();
return 0;
}
else
{
return 1;
}
}
else
{
TTF_Quit();
SDL_Quit();
return 1;
}
}
}
So it look like the game loop does the following:
- Handles user input events, updating the input buffer if a valid character is typed.
- Checks if the flag is valid by verifying it starts with
FCSC{, ends with}, and thatcheck_flag_validity()returns True. - Updates the timer and the game scene, showing a win screen if the flag is valid or an end screen after 60 seconds.
Understanding how the flag validity is checked
We’ll now focus on the check_flag_validity() function as it seems to be where everything happen.
__int64 check_flag_validity()
{
__int64 v0; // r9
unsigned int pitch; // edi
__int64 pixels; // rcx
__int64 format; // rdx
_DWORD rect[4]; // [rsp+0h] [rbp-90h] BYREF
_BYTE char_colors[68]; // [rsp+10h] [rbp-80h] BYREF
int some_pixel; // [rsp+54h] [rbp-3Ch]
__int64 orig_pixels; // [rsp+58h] [rbp-38h]
__int64 RGBSurfaceWithFormat; // [rsp+60h] [rbp-30h]
int y; // [rsp+68h] [rbp-28h]
int x; // [rsp+6Ch] [rbp-24h]
unsigned __int64 m; // [rsp+70h] [rbp-20h]
unsigned int is_flag_valid; // [rsp+7Ch] [rbp-14h]
int k; // [rsp+80h] [rbp-10h]
int j; // [rsp+84h] [rbp-Ch]
char pixel_color_index; // [rsp+8Bh] [rbp-5h]
int i; // [rsp+8Ch] [rbp-4h]
memset(char_colors, 255, 64uLL);
for ( i = 0; i <= 63; ++i )
{
x = 17 * i + 60;
y = 607;
RGBSurfaceWithFormat = SDL_CreateRGBSurfaceWithFormat(0LL, 16LL, 32LL, 32LL, 0x16462004LL);
if ( !RGBSurfaceWithFormat )
return 0LL;
pitch = *(_DWORD *)(RGBSurfaceWithFormat + 24);
pixels = *(_QWORD *)(RGBSurfaceWithFormat + 32);
format = **(unsigned int **)(RGBSurfaceWithFormat + 8);
rect[0] = x;
rect[1] = y;
rect[2] = 16;
rect[3] = 32;
((void (__fastcall *)(__int64, _DWORD *, __int64, __int64, _QWORD, __int64))SDL_RenderReadPixels)(
render_target,
rect,
format,
pixels,
pitch,
v0);
orig_pixels = *(_QWORD *)(RGBSurfaceWithFormat + 32);
pixel_color_index = -1;
for ( j = 0; j <= 31; ++j )
{
for ( k = 0; k <= 15; ++k )
{
some_pixel = *(_DWORD *)(4LL * (16 * j + k) + orig_pixels);
if ( pixel_color_index == -1 )
pixel_color_index = get_pixel_color_index(some_pixel);
}
}
char_colors[i] = pixel_color_index;
SDL_FreeSurface(RGBSurfaceWithFormat);
}
is_flag_valid = 1;
for ( m = 0LL; m <= 0x3F; ++m )
is_flag_valid = ((unsigned __int8)char_colors[m] == valid_char_colors[m]) & (unsigned __int8)is_flag_valid;
return is_flag_valid;
}
The first loop of this function do the following:
- For each of the 64 characters of the user input, it reads a 16x32 pixels rectangle from the screen using
SDL_RenderReadPixels. This rectangle contains the pixels of the rendered character. - It scans the pixels of this rectangle and finds the first pixel whose color matches a predefined color palette using the function
get_pixel_color_index. - It saves the corresponding color index in the array
char_colors.
The color palette is the following:
unsigned int colors[] = {
0xFFFFFFFF,
0x802D2FFF,
0xFF595EFF,
0xFF924CFF,
0xFFAE43FF,
0xFFCA3AFF,
0x8AC926FF,
0x52A675FF,
0x6A4C93FF,
0x1982C4FF,
};
Finally the second loop compares this array of color indices to a hardcoded array valid_char_colors. If they all match, the flag is valid.
Figuring out how the input characters colors are modified
This is the step that took me the most time, after looking everywhere in the code I did not find any place where the characters color could be changed. After looking more carefully, I realized the executable embeds a .ttf font. If we look into the game functions we see a reference to the TTF_OpenFontRW function. Looking at x-refs to it we end up in the following function:
_BOOL8 __fastcall sub_9BC6(_QWORD *a1)
{
__int64 v2; // [rsp+18h] [rbp-8h]
v2 = SDL_RWFromConstMem(&font_buffer, (unsigned int)font_buffer_size);
if ( !v2 )
return 1LL;
*a1 = TTF_OpenFontRW(v2, 1LL, 28LL);
return *a1 == 0LL;
}
This function load a font of 1249296 bytes from the .data segment. After manually extracting the .ttf font we analyze it using FontDrop. And that’s where it all becomes clearer, the font make uses of an OpenType feature known as Contextual Alternates.
This features allows the font renderer to modify characters of a rendered text based on surrounding characters. For instance this can be used to replace oe with œ. In our case, it is used to modify the color of the penultimate character based on the last typed character.
Solving the challenge
Unfortunately, I couldn’t fully reverse the contextual rules. So I chose to bruteforce it: since the color of a character only depends on the next one, and we know the last character is }, we can work backwards!.
Here is my Python script that achieve this:
from PIL import Image, ImageDraw, ImageFont
colors_bytes = bytes.fromhex(
"FFFFFFFFFF2F2D80FF5E59FFFF4C92FFFF43AEFF" \
"FF3ACAFFFF26C98AFF75A652FF934C6AFFC48219"
)
COLORS = []
for i in range(10):
# RGBA little endian
COLORS.append(
(
colors_bytes[4 * i + 3],
colors_bytes[4 * i + 2],
colors_bytes[4 * i + 1],
colors_bytes[4 * i + 0],
)
)
FONT = ImageFont.truetype(
"font.ttf", size=32, layout_engine=ImageFont.Layout.RAQM
)
CHARSET = "0123456789abcdef"
# Indices of each flag character colors in the above table
TARGET_CHAR_COLOR_INDEXES = [
0, 0, 0, 0, 0, 9, 6, 3, 6, 7, 6, 5, 7, 4, 6, 2, 7, 7, 2, 9, 6, 7, 7, 5, 1,
6, 2, 8, 4, 3, 6, 8, 5, 4, 9, 2, 9, 1, 2, 7, 1, 1, 4, 4, 2, 5, 4, 8, 6, 1,
6, 7, 4, 9, 1, 9, 5, 4, 3, 9, 9, 9, 3, 0
]
def get_character_color_index(char_img):
img_width, img_height = char_img.size
for x in range(img_width):
for y in range(img_height):
pixcol = char_img.getpixel((x, y))
for i, col in enumerate(COLORS):
if col == pixcol:
return i
def get_character_color_indexes(text):
character_color_indexes = []
image = Image.new("RGBA", (1300, 64), (255, 255, 255, 0))
draw = ImageDraw.Draw(image)
draw.text((0, 0), text, font=FONT, embedded_color=True)
y_offset = 10
x_offset = 0
char_width = 20
char_height = 32
for i in range(len(text)):
if i > 4: # letters other than FCSC{ are slightly smaller
char_width = 19.85
char_top_x = int(x_offset)
char_top_y = y_offset
char_img = image.crop(
(
char_top_x,
char_top_y,
char_top_x + char_width,
char_top_y + char_height,
)
)
character_color_indexes.append(get_character_color_index(char_img))
x_offset += char_width
return character_color_indexes
def bruteforce_characters(flag_end):
if len(flag_end) == 59:
return "FCSC{" + flag_end
candidates = []
for char in CHARSET:
text = "FCSC{" + (58 - len(flag_end)) * "a" + char + flag_end
text_character_color_indexes = get_character_color_indexes(text)
if (
text_character_color_indexes[-(len(flag_end)+1):]
== TARGET_CHAR_COLOR_INDEXES[-(len(flag_end)+1):]
):
candidates.append(char + flag_end)
for cand in candidates:
flag = bruteforce_characters(cand)
if flag is not None:
return flag
flag = bruteforce_characters("}")
print(f"[*] Flag: {flag}")
Flag: FCSC{393005dd2218ba02bfda28559813de7586c267140d08e1e83a4ae5a61d}
fcsclang
Votre collègue (entre autres aficionado du Rust) a créé un nouveau langage avant-gardiste.
Ce langage sera, à n’en pas douter, révolutionnaire pour l’industrie si tant est qu’il soit documenté.
“Pas d’inquiétude, ça se lit comme un roman” vous affirme votre collègue qui vous donne alors un crackme dans ce langage pour vous montrer la simplicité de lecture et de compréhension du langage.
Vous restez circonspect mais relevez le défi.
Solves: 26
Difficulty: ⭐⭐⭐
In this challenge we are given four files:
fcsclang: An ELF x64 executable.libfcsclang.so: An ELF x64 shared object.program.fcsc: A regular text file.Dockerfile: A Dockerfile that helps set up an environment to run thefcsclangexecutable.
The fcsclang executable acts as an interpreter for .fcsc programs. Provided the libtree-sitter.so.0.22 library is available in your environment (which should be the case if you use the provided Dockerfile), any .fcsc program can be run with:
$ ./fcsclang <program>
A first look at the main function reveals the following after renaming:
__int64 __fastcall main(__int64 argc, char **argv, char **envp)
{
__int64 fcscclang; // rax
int v5; // eax
size_t br; // rax
__int64 root_node[4]; // [rsp+10h] [rbp-F0h] BYREF
__int64 root_token; // [rsp+30h] [rbp-D0h] BYREF
unsigned int v9; // [rsp+38h] [rbp-C8h]
stat buf; // [rsp+40h] [rbp-C0h] BYREF
__int64 tree; // [rsp+D8h] [rbp-28h]
unsigned __int64 programm_size; // [rsp+E0h] [rbp-20h]
FILE *programm_file; // [rsp+E8h] [rbp-18h]
__int64 parser; // [rsp+F0h] [rbp-10h]
unsigned __int64 i; // [rsp+F8h] [rbp-8h]
if ( (int)argc > 1 )
{
parser = ts_parser_new();
fcscclang = tree_sitter_fcsclang();
ts_parser_set_language(parser, fcscclang);
programm_file = fopen(argv[1], "r");
if ( programm_file )
{
v5 = fileno(programm_file);
fstat(v5, &buf);
programm_size = buf.st_size;
programm_copy = malloc_buffer(buf.st_size);
for ( i = 0LL; i < programm_size; i += br )
br = fread(programm_copy, 1uLL, programm_size - i, programm_file);
tree = ts_parser_parse_string(parser, 0LL, programm_copy, (unsigned int)programm_size);
if ( tree )
{
global_variables = (__int64)alloc_space_for_global_variables();
scope_variables_table = (__int64)alloc_space_for_scope_variables();
get_root_node(tree, root_node);
process_node(root_node, &root_token);
free_global_variables(global_variables);
free_scope_variables((_QWORD *)scope_variables_table);
free(programm_copy);
ts_tree_delete(tree);
ts_parser_delete(parser);
return v9;
}
else
{
return 0xFFFFFFFFLL;
}
}
else
{
return 0xFFFFFFFFLL;
}
}
else
{
printf("Usage: %s <program>\n", *argv);
return 0xFFFFFFFFLL;
}
}
The interpreter uses the tree-sitter library to parse the input program using a custom language. To do so it setup a custom language parser using ts_parser_set_language(). The pointer to the custom language parser structure fcscclang is obtained by calling tree_sitter_fcsclang(), a function imported from the libfcsclang.so shared library. Thus, the entire lexing and parsing logic resides in this shared library. The executable simply interfaces with the library through the tree-sitter API to obtain a syntax tree representing the program.
Once parsed, the main function initializes memory buffers for variable storage and starts interpreting the program using the process_node function.
Analyzing the given program
Opening the given program in a text editor shows the following:
consterner I Le 24 mai 1863, un dimanche, mon oncle, le professeur Lidenbrock, revint précipitamment vers sa petite maison située au numéro 19 de Königstrasse, l’une des plus anciennes rues du vieux quartier de Hambourg. La bonne Marthe dut se croire fort
…
ce personnage lui indiqua la situation du Muséum des Antiquités du Nord. Le directeur de ce curieux établissement, où sont
It is an excerpt from Journey to the Center of the Earth by Jules Verne, doesn’t really look like a program…
Yet, it is accepted as valid input for the interpreter. Something must be hidden inside
Reversing the lexing and parsing logic in libfcsclang.so would likely be a nightmare, as it is huge and was probably automatically generated using a grammar file (as explained here).
Thanksfully, the authors of the challenge left this logic in a separate object, meaning we can use the parser in our own programm using the tree-sitter API. Furthermore, the tree-sitter API expose the very useful ts_node_string(TSNode self) , which produces a human-readable string representation of the syntax tree. We will use this to extract the program syntax tree.
Using the provided library
We first download the tree-sitter 22.0 source code from their GitHub releases. After building the library with make, we will compile the following program:
#include <assert.h>
#include <string.h>
#include <stdio.h>
#include <dlfcn.h>
#include <tree_sitter/api.h>
TSLanguage *(*tree_sitter_fcsclang)(void);
const char *FILENAME = "program.fcsc";
int load_language_lib(void) {
void *handle = dlopen("./libfcsclang.so", RTLD_NOW);
if (!handle) {
return 1;
}
tree_sitter_fcsclang = dlsym(handle, "tree_sitter_fcsclang");
const char *error = dlerror();
if (error) {
dlclose(handle);
return 1;
}
return 0;
}
char *open_program(void) {
FILE *f = fopen(FILENAME, "r");
if (!f) {
return NULL;
}
// Get the program size
fseek(f, 0, SEEK_END);
size_t size = ftell(f);
rewind(f);
// Copy it into a buffer
char *buffer = malloc(size);
if (!buffer) {
fclose(f);
return NULL;
}
size_t read = fread(buffer, 1, size, f);
if (read != size) {
free(buffer);
fclose(f);
return NULL;
}
fclose(f);
return buffer;
}
int main() {
if (load_language_lib() != 0) {
printf("[x] Error while loading language lib !\n");
return 1;
}
// Create a parser.
TSParser *parser = ts_parser_new();
printf("[*] Parser sucessfully created !\n");
ts_parser_set_language(parser, tree_sitter_fcsclang());
char *program_copy = open_program();
if (program_copy == NULL) {
printf("[x] Error while loading program !\n");
return 1;
}
printf("[*] Sucessfully loaded program in memory !\n");
TSTree *tree = ts_parser_parse_string(
parser,
NULL,
program_copy,
strlen(program_copy)
);
printf("[*] Sucessfully parsed program !\n");
TSNode root_node = ts_tree_root_node(tree);
bool has_root_node_error = ts_node_has_error(root_node);
if (has_root_node_error) {
printf("[x] Root node has an error !\n");
return 1;
}
char *string = ts_node_string(root_node);
printf("Syntax tree:\n");
printf("%s\n", string);
free(string);
ts_tree_delete(tree);
ts_parser_delete(parser);
return 0;
}
The program can be compiled using the following command line:
$ clang -I tree-sitter-0.22.0/lib/include \
extract_syntax_tree.c \
tree-sitter-0.22.0/libtree-sitter.a \
-o extract_syntax_tree
After running it, here is an extract of what we get:
(program (top_level_item (statement (expression_statement (expression (assign lvalue: (lvalue identifier: (identifier)) value: (expression (array list: (array_list element: (expression (array list: (array_list element: (expression (number_literal (digit (undocumented_732293a7c7094ffd))))
...
(statement (expression_statement (expression (number_literal (digit (undocumented_732293a7c7094ffd))))))) undocumented_75dc81fb2f8d9ce3: (scope (statement (expression_statement (expression (builtin (undocumented_0fe135eb8cd073ef param: (expression (str))))))) (statement (expression_statement (expression (number_literal (digit (undocumented_f9bfceb10223dcd6)))))))))))
Reverse-engineering undocumented node types
The syntax tree obtained previously shows a lot of reference to “undocumented” nodes. To analyze the program properly, we’ll have to figure out what they are by reverse engineering the interpreter. To do so let’s take a look at the process_node function:
void __fastcall process_node(__int64 *node, __int64 *token)
{
const char *node_type; // [rsp+18h] [rbp-8h]
if ( has_node_error(node) )
{
fwrite("Syntax error\n", 1uLL, 0xDuLL, stderr);
exit(1);
}
node_type = get_node_type(node);
if ( !strcmp(node_type, "function_definition") )
{
process_func_def(node, (__int64)token);
}
else if ( !strcmp(node_type, "number") )
{
process_number_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_732293a7c7094ffd") )
{
process_undoc1_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_f9bfceb10223dcd6") )
{
process_undoc2_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_d53cabc7357ff2a5") )
{
process_undoc3_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_210eb81a94b8b633") )
{
process_undoc4_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_c589a8f3aaff75f7") )
{
process_undoc5_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_ac7469dafc6e9c77") )
{
process_undoc6_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_8212463fe42cc213") )
{
process_undoc7_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_791df7d09856e81f") )
{
process_undoc8_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_db9dce746e821769") )
{
process_undoc9_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_ac3fcec30d0b6a40") )
{
process_undoc10_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "str") )
{
process_str_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "array") )
{
process_array_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "identifier") )
{
process_identifier_decl(node, token);
}
else if ( !strcmp(node_type, "function_call") )
{
process_func_call(node, (__int64)token);
}
else if ( !strcmp(node_type, "scope") )
{
process_scope_decl(node, token);
}
else if ( !strcmp(node_type, "lvalue") )
{
process_lvalue_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "assign") )
{
process_assign_decl(node, token);
}
else if ( !strcmp(node_type, "subscript") )
{
process_subscript_decl(node, token);
}
else if ( !strcmp(node_type, "binexp") )
{
process_binexp_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "unexp") )
{
process_unexp_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_9bfdf82a969d10c2") )
{
process_undoc11_decl((__int64)node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_af0dbc52101afc49") )
{
process_undoc12_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_0fe135eb8cd073ef") )
{
process_undoc13_decl(node, (__int64)token);
}
else if ( !strcmp(node_type, "undocumented_48359b1cc713e5a1") )
{
process_undoc14_decl(node, token);
}
else if ( !strcmp(node_type, "undocumented_c44ff70e0a035b84") )
{
process_undoc15_decl(node, token);
}
else
{
process_node_childs(node, token);
}
}
Alright, so it look like we have processing functions for each undocumented nodes. Analyzing one of these functions, for example the one for undocumented_9bfdf82a969d10c2 nodes, shows:
__int64 __fastcall process_undoc11_decl(__int64 node, __int64 token)
{
size_t n; // [rsp+18h] [rbp-18h] BYREF
char *lineptr; // [rsp+20h] [rbp-10h] BYREF
int number; // [rsp+2Ch] [rbp-4h]
lineptr = 0LL;
getline(&lineptr, &n, stdin);
number = atoi(lineptr);
free(lineptr);
return create_number_token(number, token);
}
As we can see, node type undocumented_9bfdf82a969d10c2 seems to represent a builtin function used to read an integer from stdin. Repeating this for all node types, we build the following mapping:
| Undocument node names | Reverse engineered node names |
|---|---|
| undocumented_732293a7c7094ffd | 0 |
| undocumented_f9bfceb10223dcd6 | 1 |
| undocumented_d53cabc7357ff2a5 | 2 |
| undocumented_210eb81a94b8b633 | 3 |
| undocumented_c589a8f3aaff75f7 | 4 |
| undocumented_ac7469dafc6e9c77 | 5 |
| undocumented_8212463fe42cc213 | 6 |
| undocumented_791df7d09856e81f | 7 |
| undocumented_db9dce746e821769 | 8 |
| undocumented_ac3fcec30d0b6a40 | 9 |
| undocumented_46eb8e8b7b15c3d5 | addition |
| undocumented_cfd09200be51d38f | substraction |
| undocumented_b341f271c655aaee | multiplication |
| undocumented_956dd300d7424ff3 | equal_check |
| undocumented_0162f13a50afff09 | not_equal_check |
| undocumented_a91bdbbce9e82238 | less_check |
| undocumented_589a700aed48e3a4 | greater_check |
| undocumented_2d5b46a88151170b | less_or_equal_check |
| undocumented_4c3cc3b8907e3db5 | greater_or_equal_check |
| undocumented_aa1bd5b44f53714d | logical_and |
| undocumented_0e772940f0fd3008 | logical_or |
| undocumented_13932b8a4b1bd439 | shift_left |
| undocumented_0cd2df8843187030 | shift_right |
| undocumented_b858202486aecd0f | bitwise_or |
| undocumented_24e094c9759dc06c | bitwise_and |
| undocumented_20d471e7543ce9f9 | logical_not |
| undocumented_9bfdf82a969d10c2 | read_integer |
| undocumented_af0dbc52101afc49 | |
| undocumented_0fe135eb8cd073ef | print_line |
| undocumented_48359b1cc713e5a1 | if_expression |
| undocumented_f543173dbe320d3f | condition_expression |
| undocumented_75dc81fb2f8d9ce3 | else_branch_scope |
| undocumented_f1e6bfd0a35c19db | if_branch_scope |
| undocumented_c44ff70e0a035b84 | while_expression |
| undocumented_a1a48da3b527af4e | while_body_scope |
With this we can now get a syntax tree that makes more sense, but we are still lacking something…
Recovering identifier names and string values
In the obtained syntax tree, variables, functions or function parameters are represented by an identifier node. An identifier node simply consist of a string, whose value represent the variable, function or function parameter name. However the syntax tree we obtained does not specify the name of each identifiers. This mean we cannot distinguish which variable is accessed or which function is called. Unfortunately the tree-sitter API does not permit to add this information to the generated syntax tree. So we will do it ourselves. To do so we modify our previous C program not to print the syntax tree, but rather to recursively iterate over the syntax tree and print each identifier names:
//...
void print_node_of_type(TSNode node, char* node_type, char *program_copy) {
const char *type = ts_node_type(node);
if (strcmp(type, node_type) == 0) {
uint32_t start = ts_node_start_byte(node);
uint32_t end = ts_node_end_byte(node);
char *node_bytes = strndup((const char *)program_copy + start, (int)(end - start));
printf("%s\n", node_bytes);
}
// Recursively iterate over the node childs
uint32_t count = ts_node_child_count(node);
for (uint32_t i = 0; i < count; i++) {
TSNode child = ts_node_child(node, i);
print_node_of_type(child, node_type, program_copy);
}
}
// ...
int main() {
// ...
TSNode root_node = ts_tree_root_node(tree);
// ...
print_node_of_type(root_node, "identifier", program_copy);
// ...
}
We compile the program as previously. When running it, we get the following:
$ ./extract_identifiers_name
[*] Parser sucessfully created !
[*] Sucessfully loaded program in memory !
[*] Sucessfully parsed program !
[*] Root node type: program
consterner
routine
inattendu
inoffensif
...
Alright, so we were able to extract each identifier names. We’ll do the exact same thing but for nodes of type str so that we can have the string values information in our exported syntax tree. Once everything is correctly exported, we use the following Python script to populate the original syntax tree with our new informations:
renamed_nodes = [
("undocumented_732293a7c7094ffd", "0"),
# ...
("undocumented_a1a48da3b527af4e", "while_body_scope")
]
with open('syntax_tree.txt', 'r') as f:
tree = f.read()
with open('identifier_names.txt', 'r') as f:
identifiers = [l.strip() for l in f.readlines() if l.strip()]
with open('strings.txt', 'r') as f:
strings = [l.strip() for l in f.readlines() if l.strip()]
for node, renamed_node in renamed_nodes:
tree = tree.replace(node, renamed_node)
for identifier in identifiers:
tree = tree.replace("(identifier)", f'("{identifier}")', 1)
for string in strings:
tree = tree.replace("(str)", f'({string})', 1)
with open('populated_syntax_tree.txt', 'w') as f:
f.write(tree)
Now we have a fully populated syntax tree with everything needed to reverse the given program !
Reverse engineering the program from its syntax tree
The syntax tree is quite large, and manually analyzing it would be tedious. Since it is a structured tree containing all necessary information, it should be fairly easy for a LLM to do it for us. Using ChatGPT, we manage to extract a pseudo code of our program in C, and after a bit of reversing we obtain the following:
int constraints_grid[9][9] = {
{0, 0, 0, 0, 0, 0, 0, 1, 8},
{0, 0, 5, 6, 1, 0, 0, 2, 0},
{3, 0, 0, 0, 0, 0, 5, 1, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 2},
{1, 0, 0, 0, 3, 0, 0, 4, 4},
{0, 0, 0, 0, 2, 1, 0, 0, 5},
{0, 0, 0, 0, 4, 3, 0, 6, 1},
{3, 1, 0, 1, 0, 6, 0, 0, 0},
{0, 0, 4, 7, 0, 0, 0, 6, 7},
};
int user_grid[9][9] = {0};
// ...
int (*get_cross_indices(int x, int y, int target_cell))[2] {
static int cross_indices[4][2] = {
{0, 0},
{0, 0},
{0, 0},
{0, 0}
};
cross_indices[0][0] = x + target_cell;
cross_indices[0][1] = y;
cross_indices[1][0] = x - target_cell;
cross_indices[1][1] = y;
cross_indices[2][0] = x;
cross_indices[2][1] = y + target_cell;
cross_indices[3][0] = x;
cross_indices[3][1] = y - target_cell;
return cross_indices;
}
int check_cross_cells(int user_grid[9][9], int x, int y, int target_cell) {
int valid = 0;
int (*cross_indices)[2] = get_cross_indices(x, y, target_cell);
int z = 0;
while (z < 4) {
int x = cross_indices[z][0];
int y = cross_indices[z][1];
if ((x >= 0 && x < 9) && (y >= 0 && y < 9)) {
if (user_grid[x][y] == target_cell) {
valid = 1;
}
}
z += 1;
}
return valid;
}
int last_sudoku_constraint(int user_grid[9][9], int constraints_grid[9][9]) {
int x = 0;
int valid = 1;
while (x < 9) {
int y = 0;
while (y < 9) {
int target_cell = constraints_grid[x][y];
if (target_cell != 0) {
valid = check_cross_cells(user_grid, x, y, target_cell) && valid;
}
y = y + 1;
}
x = x + 1;
}
return valid;
}
int is_grid_valid(int user_grid[9][9], int constraint_grid[9][9]) {
int valid = are_sudoku_grid_lines_valid(user_grid);
valid = are_sudoku_grid_columns_valid(user_grid) && valid;
valid = are_sudoku_grid_squares_valid(user_grid) && valid;
valid = last_sudoku_constraint(user_grid, constraints_grid) && valid;
return valid;
}
int main(void) {
get_user_input_grid(user_grid);
if (is_grid_valid(user_grid, constraints_grid)) {
display_flag_from_grid(user_grid);
return 0;
} else {
printf("No\n");
return 1;
}
}
Note: Not all functions are included for the sake of brevity; they consist of regular Sudoku-checking functions.
What this program seems to do is read a 9x9 Sudoku grid from the user input, verify whether it is a valid Sudoku grid, and check one final condition using the last_sudoku_constraint function. If the grid satisfies all the constraints, the flag is printed using the values of each grid cell.
Solving the final puzzle
The last sudoku constraint is where everything happens. Essentially, it consists of the following:
If a cell of constraints_grid is not zero, for example, 3, it checks that either:
- The cell located 3 tiles above is equal to 3.
- The cell located 3 tiles below is equal to 3.
- The cell located 3 tiles to the left is equal to 3.
- Or the cell located 3 tiles to the right is equal to 3.
If any of these four cells fall outside the Sudoku grid, they are simply ignored.
Now that we understand the idea behind this constraint, we can write a Z3 solver script to solve the problem and recover the flag:
from z3 import *
def solve_cross_sudoku(constraints_grid):
grid = [[Int(f"cell_{i}_{j}") for j in range(9)] for i in range(9)]
s = Solver()
# Each cell contains a digit from 1 to 9
for i in range(9):
for j in range(9):
s.add(grid[i][j] >= 1, grid[i][j] <= 9)
# Unique digits in each row
for i in range(9):
s.add(Distinct([grid[i][j] for j in range(9)]))
# Unique digits in each column
for j in range(9):
s.add(Distinct([grid[i][j] for i in range(9)]))
# Unique digits in each 3×3 block
for block_i in range(3):
for block_j in range(3):
s.add(
Distinct(
[
grid[3 * block_i + i][3 * block_j + j]
for i in range(3)
for j in range(3)
]
)
)
# Last custom "cross" constraints
for x in range(9):
for y in range(9):
v = constraints_grid[x][y]
if v != 0:
cross_indices = [
(x + v, y),
(x - v, y),
(x, y + v),
(x, y - v),
]
valid_indices = []
for x_ind, y_ind in cross_indices:
if (0 <= x_ind < 9) and (0 <= y_ind < 9):
valid_indices.append((x_ind, y_ind))
s.add(
Or(
[
grid[indx][indy] == v
for (indx, indy) in valid_indices
]
)
)
if s.check() == sat:
m = s.model()
solution = [[m[grid[i][j]].as_long() for j in range(9)] for i in range(9)]
return solution
else:
return None
def print_flag(grid):
flag = "FCSC{"
for x in range(9):
for y in range(9):
flag += str(grid[x][y])
print(flag + "}")
constraints_grid = [
[0, 0, 0, 0, 0, 0, 0, 1, 8],
[0, 0, 5, 6, 1, 0, 0, 2, 0],
[3, 0, 0, 0, 0, 0, 5, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 2],
[1, 0, 0, 0, 3, 0, 0, 4, 4],
[0, 0, 0, 0, 2, 1, 0, 0, 5],
[0, 0, 0, 0, 4, 3, 0, 6, 1],
[3, 1, 0, 1, 0, 6, 0, 0, 0],
[0, 0, 4, 7, 0, 0, 0, 6, 7],
]
solution = solve_cross_sudoku(constraints_grid)
print_flag(solution)
Flag:FCSC{836219754549786312127345968658193427314827695792564831965471283481632579273958146}
alfheim
Trouver l’entrée acceptée par le binaire.
Solves: 22
Difficulty: ⭐⭐⭐
In this challenge, we’re given an x64 ELF binary that expects some input. Let’s take a look at the main function:
int __fastcall main(int argc, const char **argv, const char **envp)
{
char user_input_buffer[32]; // [rsp+10h] [rbp-60h] BYREF
char v5; // [rsp+30h] [rbp-40h]
_QWORD unxored_buffer[5]; // [rsp+40h] [rbp-30h] BYREF
int i; // [rsp+6Ch] [rbp-4h]
memset(unxored_buffer, 0, 32);
memset(user_input_buffer, 0, sizeof(user_input_buffer));
v5 = 0;
fgets(user_input_buffer, 33, stdin);
for ( i = 0; i <= 31; ++i )
*((_BYTE *)unxored_buffer + i) = xor_table[i] ^ user_input_buffer[i];
if ( !memcmp(unxored_buffer, &target_val, 0x20uLL) )
printf("Well done! The flag is FCSC{%s}\n", user_input_buffer);
else
puts("Invalid input :(");
return 0;
}
Easy, right?
$ ./alfheim
6cb381c59845ff5e2a774f6e3ed60bed
█████ ███ █████
░░███ ░███ ░░███
░███ ░███ ░███ ████████ ██████ ████████ ███████
░███ ░███ ░███ ░░███░░███ ███░░███░░███░░███ ███░░███
░░███ █████ ███ ░███ ░░░ ░███ ░███ ░███ ░███ ░███ ░███
░░░█████░█████░ ░███ ░███ ░███ ░███ ░███ ░███ ░███
░░███ ░░███ █████ ░░██████ ████ █████░░███████
░░░ ░░░ ░░░░░ ░░░░░░ ░░░░ ░░░░░ ░░░░░███
███ ░███
░░██████
░░░░░░
█████ █████ █████ █████ ███
░░███ ░░███ ░░███ ░░███ ░░░
░███ ████████ ███████ ██████ ████████ ████████ ████████ ██████ ███████ ██████ ███████ ████ ██████ ████████
░███ ░░███░░███ ░░░███░ ███░░███░░███░░███░░███░░███░░███░░███ ███░░███░░░███░ ░░░░░███ ░░░███░ ░░███ ███░░███░░███░░███
░███ ░███ ░███ ░███ ░███████ ░███ ░░░ ░███ ░███ ░███ ░░░ ░███████ ░███ ███████ ░███ ░███ ░███ ░███ ░███ ░███
░███ ░███ ░███ ░███ ███░███░░░ ░███ ░███ ░███ ░███ ░███░░░ ░███ ███ ███░░███ ░███ ███ ░███ ░███ ░███ ░███ ░███
█████ ████ █████ ░░█████ ░░██████ █████ ░███████ █████ ░░██████ ░░█████ ░░████████ ░░█████ █████░░██████ ████ █████
░░░░░ ░░░░ ░░░░░ ░░░░░ ░░░░░░ ░░░░░ ░███░░░ ░░░░░ ░░░░░░ ░░░░░ ░░░░░░░░ ░░░░░ ░░░░░ ░░░░░░ ░░░░ ░░░░░
░███
█████
░░░░░
Hmm, not quite. Let’s see where this message is printed.
$ strace --stack-trace ./alfheim
execve("./alfheim", ["./alfheim"], 0x7ffe1400dc38 /* 76 vars */) = 0
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x390f0]
> unexpected_backtracing_error [0x1]
read(0, 6cb381c59845ff5e2a774f6e3ed60bed
"6cb381c59845ff5e2a774f6e3ed60bed"..., 4096) = 33
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39977]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39dc2]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x390f0]
> unexpected_backtracing_error [0x7ffcdd5d3308]
write(1, "long ascii art fail msg", 3973
) = 3973
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x3947d]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39929]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39981]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39dc2]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x390f0]
> unexpected_backtracing_error [0x7ffcdd5d3308]
write(1, "\n", 1
) = 1
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39498]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39929]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39981]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x39dc2]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim() [0x390f0]
> unexpected_backtracing_error [0x7ffcdd5d3308]
exit(0) = ?
+++ exited with 0 +++
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim(+0x5d) [0x39939]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim(+0x43) [0x39981]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim(+0x2e0) [0x39dc2]
> /home/user/CTF/FCSC2025/reverse/alfheim/alfheim(+0x0) [0x390f0]
> unexpected_backtracing_error [0x7ffcdd5d3308]
The code at 0x390f0 seems to be a regular ELF start function:
void __fastcall __noreturn start(__int64 a1, __int64 a2, void (*a3)(void))
{
__int64 v3; // rax
int v4; // esi
__int64 v5; // [rsp-8h] [rbp-8h] BYREF
char *retaddr; // [rsp+0h] [rbp+0h] BYREF
v4 = v5;
v5 = v3;
_libc_start_main((int (*)(int, char **, char **))main, v4, &retaddr, 0LL, 0LL, a3, &v5);
__halt();
}
However 0x39dc2 is not the main function IDA shows ….
__int64 __fastcall sub_439AE2(
__int64 a1,
__int64 a2,
__int64 a3,
__int64 a4,
__int64 a5,
__int64 a6,
__int64 a7,
__int64 a8,
__int64 a9)
{
__int64 v10; // [rsp+20h] [rbp-70h]
__int64 v11; // [rsp+28h] [rbp-68h]
unsigned __int64 v12; // [rsp+30h] [rbp-60h]
unsigned __int64 v13; // [rsp+38h] [rbp-58h]
unsigned __int64 v14; // [rsp+40h] [rbp-50h]
__int64 v15; // [rsp+48h] [rbp-48h]
__int64 v16; // [rsp+50h] [rbp-40h]
__int64 v17; // [rsp+58h] [rbp-38h]
unsigned __int16 j; // [rsp+66h] [rbp-2Ah]
_QWORD *v19; // [rsp+68h] [rbp-28h]
void *v20; // [rsp+70h] [rbp-20h]
unsigned __int16 v21; // [rsp+7Eh] [rbp-12h]
__int64 v22; // [rsp+80h] [rbp-10h]
__int64 *i; // [rsp+88h] [rbp-8h]
_QWORD *v24; // [rsp+88h] [rbp-8h]
__int64 savedregs; // [rsp+90h] [rbp+0h] BYREF
_UNKNOWN *retaddr; // [rsp+98h] [rbp+8h]
for ( i = &savedregs + a9 + 6; *i; ++i )
;
v24 = i + 1;
v22 = 0LL;
v21 = 0;
v20 = 0LL;
while ( *v24 )
{
switch ( *v24 )
{
case 3LL:
v22 = v24[1];
break;
case 5LL:
v21 = v24[1];
break;
case 9LL:
v20 = (void *)v24[1];
break;
}
v24 += 2;
}
retaddr = v20;
for ( j = 0; j < v21; ++j )
{
if ( *(_DWORD *)v22 == 2 )
v19 = *(_QWORD **)(v22 + 16);
v22 += 56LL;
}
v17 = 0LL;
v16 = 0LL;
v15 = 0LL;
v14 = 0LL;
v13 = 0LL;
v12 = 0LL;
v11 = 0LL;
v10 = 0LL;
while ( *v19 )
{
switch ( *v19 )
{
case 6LL:
v17 = v19[1];
break;
case 5LL:
v11 = v19[1];
break;
case 7LL:
v16 = v19[1];
break;
case 0x17LL:
v15 = v19[1];
break;
case 8LL:
v13 = v19[1];
break;
case 2LL:
v12 = v19[1];
break;
case 9LL:
v14 = v19[1];
break;
case 0x6FFFFEF5LL:
v10 = v19[1];
break;
}
v19 += 2;
}
sub_439348(v17, v11, v10, v16, (unsigned int)(v13 / v14));
sub_439348(v17, v11, v10, v15, (unsigned int)(v12 / v14));
return sub_43993E(v17, v10, v15, (unsigned int)(v12 / v14));
}
There’s definitely something strange going on…
Figuring out what’s happening
After a bit of dynamic and static reversing, we realize that the first loop in sub_439AE2 (which we’ll now call real_main) parses the .dynamic section of the ELF (at 0x45ddf8) and sets the following variables:
v17: ELF Symbol Table address (DT_SYMTAB)v11: ELF String Table address (DT_STRTAB)v10: ELF GNU Hash Table address (DT_GNU_HASH)v16: ELF RELA Relocation Table address (DT_RELA)v15: ELF JMPREL Relocation Table address (DT_JMPREL)v13: ELF RELA Relocation Table size (DT_RELASZ)v12: Total size of the relocation entries associated with the procedure linkage table (DT_PLTRELSZ)v14: The size, in bytes, of aDT_RELArelocation entry (DT_RELAENT)
Then it calls sub_439348 twice, once with the RELA table address and once with the JMPREL table address. Let’s look at this mysterious sub_439348 function. After quite some times reversing it, retyping variables we come up with the following:
__int64 __fastcall reloc_symbols_using_gnu_hash_table(
__int64 symtab_ptr,
__int64 strtab_ptr,
gnu_hash_table *elf_gnu_hash_table_ptr,
Elf64_Rela *reloc_table_entry,
unsigned int number_of_entry)
{
__int64 result; // rax
__int64 replacement_func; // [rsp+28h] [rbp-30h]
char *symbol_str_addr; // [rsp+30h] [rbp-28h]
unsigned __int64 i; // [rsp+48h] [rbp-10h]
for ( i = 0LL; ; ++i ) // Iterate over eah entry of the relocation table
{
result = number_of_entry;
if ( i >= number_of_entry )
break;
*(_QWORD *)reloc_table_entry->r_offset = ret_minus1_func; // dummy function that return -1
symbol_str_addr = (char *)(*(unsigned int *)(24 * HIDWORD(reloc_table_entry->r_info) + symtab_ptr) + strtab_ptr);
// symtab_ptr+sizeof(Elf64_Sym)*(relocation_table_ptr->r_info >> 16) points to
// an Elf64_Sym structure. So dereferencing it give sym->st_name and
// STRTAB + sym->st_name point to the string that contains the symbol name.
// If the symbol name is not null, aka for fgets, memcmp then it replace the
// symbol address with the one found in the gnu hash table
if ( *symbol_str_addr )
{
replacement_func = gnu_lookup(symtab_ptr, elf_gnu_hash_table_ptr, symbol_str_addr);
if ( replacement_func )
*(_QWORD *)reloc_table_entry->r_offset = replacement_func;
}
++reloc_table_entry;
}
return result;
}
What this function does is that it iterates over each entry of the relocation table passed as argument, and, for each entry, check the symbol name of the entry in the String Table by derenferencing many ELF internal structure. If the symbol name is non-null (e.g. fgets, memcmp), it replaces the function pointer with a new address found via a GNU hash table lookup. If the symbol is not in the hash table, it replaces it with a dummy function that simply returns -1. The GNU hash table is a simple hash table that map symbol names to symbol address, this very nice article explain in detail how it works.
To summarize, when launching the executable, the function that actually runs first is not main, but this real_main function that replace every symbol addresses either by another function queried from the GNU hash table or by a dummy function that return -1.
Next, it calls sub_43993E, which is where our input is truly processed, here is its source code:
__int64 __fastcall reloc_symbols_from_user_input(
__int64 symtab_ptr,
unsigned int *elf_gnu_hash_table_ptr,
__int64 ELF_JMPREL_Relocation_Table_ptr,
unsigned int relocation_entry_count)
{
signed __int64 br; // rax
__int64 dash_index; // rax
char *after_dash_str; // [rsp+38h] [rbp-38h]
int reloc_entry_index; // [rsp+44h] [rbp-2Ch]
__int64 dash_index_copy; // [rsp+48h] [rbp-28h]
_BYTE *end_reloc_replace_info; // [rsp+50h] [rbp-20h]
char *group_ptr; // [rsp+60h] [rbp-10h]
int previous_reloc_entry_index; // [rsp+68h] [rbp-8h]
int replacement_done; // [rsp+6Ch] [rbp-4h]
br = sys_read(0, user_input_buf, 0x1000uLL); // read 0x1000 bytes from stdin
is_input_fake_flag((__int64)user_input_buf);
dash_index = (__int64)get_index_of(user_input_buf, '\n'); // get first newline index
if ( dash_index )
*(_BYTE *)dash_index = 0;
replacement_done = 0;
previous_reloc_entry_index = 0;
for ( group_ptr = user_input_buf; replacement_done <= 510; group_ptr = end_reloc_replace_info + 1 )
{
end_reloc_replace_info = get_index_of(group_ptr, ';');
if ( end_reloc_replace_info )
*end_reloc_replace_info = 0; // remove the semicolon
dash_index = (__int64)get_index_of(group_ptr, '-');
dash_index_copy = dash_index;
if ( !dash_index )
break;
*(_BYTE *)dash_index = 0; // remove the dash
reloc_entry_index = three_hexchars_to_int(group_ptr);
dash_index = dash_index_copy + 1;
after_dash_str = (char *)(dash_index_copy + 1);
if ( reloc_entry_index < 0 )
break;
dash_index = (unsigned int)reloc_entry_index;
if ( reloc_entry_index >= relocation_entry_count ) // reloc indexes should be sorted
break;
dash_index = (unsigned int)reloc_entry_index;
if ( reloc_entry_index < previous_reloc_entry_index )
break;
dash_index = sum_3digit_mod_two(after_dash_str);
if ( !(_DWORD)dash_index )
break; // sum of digits must be equal to 1 mod 2, useless check
dash_index = gnu_lookup(symtab_ptr, elf_gnu_hash_table_ptr, after_dash_str);
if ( !dash_index ) // check that replacement func exists
break;
**(_QWORD **)(24LL * reloc_entry_index + ELF_JMPREL_Relocation_Table_ptr) = dash_index; // replace the function
dash_index = (unsigned int)reloc_entry_index;
previous_reloc_entry_index = reloc_entry_index;
++replacement_done;
if ( !end_reloc_replace_info )
break;
dash_index = (__int64)(end_reloc_replace_info + 1); // jump to the next relocation string
}
return dash_index;
}
4096 bytes are read from the standard input using the read() syscall. Then this input is checked against the fake 6cb381c59845ff5e2a774f6e3ed60bed flag by the is_input_fake_flag function. This is where the above ASCII art comes from !
Afterward, the function parses the input looking for patterns like XXX-YYY;:
XXXis an uppercase hexadecimal number and represents an index in the JMPREL relocation table.YYYis a three-letter uppercase string used as a key to look up a function address via the GNU hash table.
The function replaces the symbol address of the relocation entry at index XXX in the JMPREL relocation table with the address of the function found via YYY in the GNU hash table. This process can happen up to 511 times.
At this point, one may wonder what is the purpose of modifying symbol addresses based on user input. Remember, the main function, which runs after all these patches, does the following:
int __fastcall main(int argc, const char **argv, const char **envp)
{
char user_input_buffer[32]; // [rsp+10h] [rbp-60h] BYREF
char v5; // [rsp+30h] [rbp-40h]
_QWORD unxored_buffer[5]; // [rsp+40h] [rbp-30h] BYREF
int i; // [rsp+6Ch] [rbp-4h]
memset(unxored_buffer, 0, 32);
memset(user_input_buffer, 0, sizeof(user_input_buffer));
v5 = 0;
fgets(user_input_buffer, 33, stdin);
for ( i = 0; i <= 31; ++i )
*((_BYTE *)unxored_buffer + i) = xor_table[i] ^ user_input_buffer[i];
if ( !memcmp(unxored_buffer, &target_val, 0x20uLL) )
printf("Well done! The flag is FCSC{%s}\n", user_input_buffer);
else
puts("Invalid input :(");
return 0;
}
The key observation here is that fgets, memcmp, printf and puts have been replaced by other functions by the real_main function. In order to retrieve the real functions they are replaced with I re-implemented the GNU hash table in Python based on the previously mentionned article.
class GnuHashTable:
def __init__(self, data):
self.nbuckets = int.from_bytes(data[0:4], 'little')
self.symoffset = int.from_bytes(data[4:8], 'little')
self.bloom_size = int.from_bytes(data[8:12], 'little')
self.bloom_shift = int.from_bytes(data[12:16], 'little')
self.bloom = []
self.buckets = []
self.chain = []
offset = 16
for _ in range(self.bloom_size):
self.bloom.append(int.from_bytes(data[offset:offset+8], 'little'))
offset += 8
for _ in range(self.nbuckets):
self.buckets.append(int.from_bytes(data[offset:offset+4], 'little'))
offset += 4
while offset != len(data):
self.chain.append(int.from_bytes(data[offset:offset+4], 'little'))
offset += 4
def gnu_hash(self, name):
h = 5381
for c in name:
h = (h*33 + c) & 0xFFFFFFFF
return h
def lookup(self, name):
name = name.encode()
namehash = self.gnu_hash(name)
symix = self.buckets[namehash % self.nbuckets]
if symix < self.symoffset:
return None
while True:
hash_ = self.chain[symix - self.symoffset]
# if only the last bit differ
if (hash_ ^ namehash <= 1):
return 0x402c58 + 8 + 24*symix
if hash_ & 1:
break
symix += 1
return None
if __name__ == "__main__":
with open('alfheim', 'rb') as f:
ght_data = f.read()[0x3B0:0x2C58]
gnu_hash_table = GnuHashTable(ght_data)
print('printf', hex(gnu_hash_table.lookup('printf')))
print('memcmp', hex(gnu_hash_table.lookup('memcmp')))
print('puts', hex(gnu_hash_table.lookup('puts')))
print('fgets', hex(gnu_hash_table.lookup('fgets')))
We get the following addresses:
printf 0x411618
memcmp 0x412848
puts 0x40f590
fgets 0x40f8a8
fgets and puts, are simply replaced by regular read and write syscall, nothing too fancy. However printf and memcmp are a bit differents. Here is what they look like:
__int64 new_printf()
{
char congrats_msg[96]; // [rsp+10h] [rbp-F0h] BYREF
_BYTE flag_buffer[32]; // [rsp+70h] [rbp-90h] BYREF
_BYTE sha256_ctx[112]; // [rsp+90h] [rbp-70h] BYREF
strcpy(congrats_msg, "Well done! The flag is FCSC{xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx}");
init_sha256((__int64)sha256_ctx);
do_sha256((__int64)sha256_ctx, (__int64)user_input_buf, 0xFF8uLL);
compute_sha256_digest((__int64)sha256_ctx, (__int64)flag_buffer);
buffer_to_hex_repr((__int64)flag_buffer, (__int64)&congrats_msg[28]);
return new_puts(congrats_msg);
}
_BOOL8 new_memcmp()
{
return nullsub_184(0) != 0;
}
If we ever manage to call printf then the flag is computed from our input and displayed using the puts replacement function. In order to do so we would need new_memcmp() to return 0, i.e. having nullsub_184(0) to return 0. But what is this nullsub_184() function doing ?
The answer is that it returns -1 !
In fact this function is accessed by jumping into the .got.plt section, but because of the symbol address replacement previously achieved by the real_main function, this function is now replaced by the ret_minus1_func function. This mean it isn’t possible to have nullsub_184(0) == 0… But remember, we can also replace symbol addresses using our input !!!
The real challenge
Our goal will be to craft an input that allow to replace nullsub_184() with a function that returns 0. Unfortunately, there is no function in the binary that simply returns 0. But, 1280 functions are available via the GNU hash table, and we find they all follow two patterns.
The first group of function, that we will call node functions, have the following structure:
__int64 __fastcall sub_439EAB(__int64 a1)
{
__int64 v2; // [rsp+10h] [rbp-10h]
v2 = nullsub_1095(a1 | 0x3500000000LL);
return nullsub_276(a1 | 0x5700000000LL) | v2;
}
They basically return
$$f_1(x \mid c_1) \mid f_2(x \mid c_2)$$where \(x\) is the input value, \((f_1, f_2)\) are two functions to be replaced using the GNU hash table and \((c_1, c_2)\) are two constants whose only one byte is not zero. One important thing to notice is that the non-null byte of both constants is always the same.
On other hand the second group of function, that we will call leaf functions, share the following structure:
_BOOL8 __fastcall sub_43B43A(__int64 a1)
{
return a1 != 0xE511A24DA53947FLL;
}
They simply compares the input to a hardcoded 64-bit constant.
Our goal is now to combine those two types of functions to produce a function that returns 0 when evaluated at input 0. The easiest way to tackle this problem is to represent it using a binary tree. Let’s use a toy example to give a concrete idea of the problem.
With the following functions, it is easy to verify that we indeed have \(f_1(0)=0\):
$$ f_1(x) = f_2(x \mid c_1^{(1)}) \mid f_3(x \mid c_2^{(1)}) = f_2(x \mid 0xAB00) \mid f_3(x \mid 0xCD00) \\ f_2(x) = f_2(x \mid c_1^{(2)}) \mid f_3(x \mid c_2^{(2)}) = f_4(x \mid 0x0011) \mid f_5(x \mid 0x0022) \\ f_3(x) = f_2(x \mid c_1^{(3)}) \mid f_3(x \mid c_2^{(3)}) = f_6(x \mid 0x0033) \mid f_7(x \mid 0x0044) \\ f_4(x) = x \text{ != } 0xAB11 \\ f_5(x) = x \text{ != } 0xAB22 \\ f_6(x) = x \text{ != } 0xCD33 \\ f_7(x) = x \text{ != } 0xCD44 \\ $$In fact:
$$ \begin{aligned} f_2(0 \mid 0xAB00) &= f_4(0xAB00 \mid 0x0011) \mid f_5(0xAB00 \mid 0x0022) \\ &= (0xAB11 \text{ != } 0xAB11) \mid (0xAB22 \text{ != } 0xAB22) \\ &= 0 \mid 0 \\ &= 0 \end{aligned} $$The same result hold for \(f_3(0 \mid 0xCD00)\) so we have \(f_1(0)=0\) .
Now that we have a concrete idea of the problem, let’s jump back to the challenge. Our goal is to find the node and leaf functions of such a binary tree to craft a function \(f\) such that \(f(0)=0\). An analysis of the executable shows that there are exactly 256 leaf functions available. It most likely means we will have to build a binary tree with 256 leaves, hence \(2\times256-1=511\) nodes.
511 … Doesn’t that remind you of anything ? That’s exactly the max amount of function replacement we are allowed to do with our input. Look like we are on the right track…
Twin leaves
Given that each pairs of leaves have a common parent node that only modify one byte of its input, each leaf function should have what we call a twin leaf. This twin leaf is a leaf function whose comparison constant only differ by one byte with it’s twin. In fact we can verify that each of the leaf function of the binary has exactly one twin leaf. Furthermore, we notice that the byte that differ is always the least significant byte. What this mean is that the level 7 nodes function shown on the image above are only node functions whose two constants affect the first byte of the input. Similarly after a quick analysis, we understand that each level of the tree is responsible for the change of one byte in the input. Our intuition could tell us that the level 6 modify the second byte of the input, the level 5 modify the third byte of the input and so on … We’ll see this is not true later. Let’s start writting our solution. First we create two classes for convenience:
class TreeLeaf:
def __init__(self, addr, cst):
self.addr = addr # leaf function address
self.cst = cst # comparison constant
self.parent_node = None # parent node function
def nth_parent_node(self, n):
assert self.parent_node is not None
if n == 1:
return self.parent_node
else:
return self.parent_node.nth_parent_node(n-1)
class TreeNode:
def __init__(self, addr, func1, func2, c1, c2):
self.addr = addr # node function address
self.func1 = func1 # func1 address
self.func2 = func2 # func2 address
self.c1 = c1 # func1 or constant
self.c2 = c2 # func2 or constant
self.parent_node = None # parent node function
@classmethod
def from_data(cls, data):
addr, (func1, c1), (func2, c2) = data
return cls(addr, func1, func2, c1, c2)
def nth_parent_node(self, n):
assert self.parent_node is not None
if n == 1:
return self.parent_node
else:
return self.parent_node.nth_parent_node(n-1)
Then we create a function responsible for finding all pairs of twin leaves. This function takes an array of tuples describing each leaf function. This data was exported from the executable using an IDA script provided at the end of this solution.
def reconstruct_twin_leaves(leafs_data):
twins = []
for i, (addr_leaf_1, d1) in enumerate(leafs_data):
for j, (addr_leaf_2, d2) in enumerate(leafs_data):
# j > i to avoid dubplicate (ie pairs (x, y) = (y, x))
if (i != j and j > i):
d = get_num_bytes_differs(d1, d2)
if d == 1:
twins.append(
(TreeLeaf(addr_leaf_1, d1), TreeLeaf(addr_leaf_2, d2))
)
return twins
Now, we need to find the parent function for each pair of leaves. This parent function must satisfy two conditions:
It should be a function that modifies only the least significant byte of the input, as previously explained.
If we denote \(d_1\) (resp. \(d_2\)) the comparison constant of the first leaf function (resp. second leaf function) and (\(c_1, c_2\)) the two constants used by the parent function to modify the input then we should have:
$$ \begin{align} \text{Byte}_0(x \mid c_1) &= c_1 = \text{Byte}_0(d_1) \\ \text{Byte}_0(x \mid c_1) &= c_2 = \text{Byte}_0(d_2) \\ \end{align} $$Note: \(\text{Byte}_0(x \mid c_1) = c_1\) because the upper levels of the tree did not modify the first byte of the input (which remains zero).
In Python, implementing a function to find the parent function for each pair of leaves yields the following:
def find_twin_leaves_parent_node(twin_leaf, possible_nodes, reloc_change_dict):
valid_parent_nodes = 0 # should be equal to 1 at the end of the loop
leaf1, leaf2 = twin_leaf
for node in possible_nodes:
# At this stage the lsb byte of the input as not yet been
# "or"-ed with anything else, so it is still 0
x = 0
if node.c1 == (leaf1.cst & 0xFF) and node.c2 == (leaf2.cst & 0xFF):
reloc_change_dict[node.func1] = leaf1.addr
reloc_change_dict[node.func2] = leaf2.addr
leaf1.parent_node = node
leaf2.parent_node = node
valid_parent_nodes += 1
elif node.c1 == (leaf2.cst & 0xFF) and node.c2 == (leaf1.cst & 0xFF):
reloc_change_dict[node.func1] = leaf2.addr
reloc_change_dict[node.func2] = leaf1.addr
leaf1.parent_node = node
leaf2.parent_node = node
valid_parent_nodes += 1
if valid_parent_nodes == 0:
raise ValueError(
"Error, could not find a parent node function for twin leaves",
leaf1,
leaf2,
)
elif valid_parent_nodes != 1:
raise ValueError(
"Multiple parent node functions found for for twin leaves",
leaf1,
leaf2,
)
Note: In this code, reloc_change_dict is a dictionary that tracks all the relocations we will need to encode in our final input.
Before going further let’s examine the leaves constants:
Different values at index 0: 256
Different values at index 1: 32
Different values at index 2: 8
Different values at index 3: 64
Different values at index 4: 2
Different values at index 5: 4
Different values at index 6: 16
Different values at index 7: 128
We observe that the eighth byte of each of the 256 leaf constants can take 128 distinct values. This indicates that the level 6 functions in the tree are responsible for modifying the eighth byte of the input, as each node affects the eighth byte of exactly two leaf constants. Similarly, the level 5 functions modify the fourth byte of the input, and so on throughout the tree structure.
With this understanding, we can now implement a function to identify the n-th parent node of a pair of twin leaves. The approach involves finding a function whose constant mask has a non-zero byte matching the corresponding byte in the leaf constants.
def find_twin_leaves_nth_parent_node(
twin_leaves, possible_nodes, byte_index, n, reloc_change_dict
):
leaf1, leaf2 = twin_leaf
valid_nth_parent_nodes = 0
target_constant = leaf1.cst & (0xFF << (8 * byte_index))
for node in possible_nodes:
if node.c1 == target_constant:
sub_node = leaf1.nth_parent_node(n - 1)
reloc_change_dict[node.func1] = sub_node.addr
sub_node.parent_node = node
valid_nth_parent_nodes += 1
elif node.c2 == target_constant:
sub_node = leaf1.nth_parent_node(n - 1)
reloc_change_dict[node.func2] = sub_node.addr
sub_node.parent_node = node
valid_nth_parent_nodes += 1
if valid_nth_parent_nodes == 0:
raise ValueError(
f"Error, could not find the {n}-th parent node function for twin leaves",
leaf1,
leaf2,
)
elif valid_nth_parent_nodes != 1:
raise ValueError(
f"Multiple {n}-th parent node functions found for twin leaves",
leaf1,
leaf2,
)
Now that we have everything needed, we can reconstruct the entire tree to find out all the relocations we need to encode in our final input:
if __name__ == "__main__":
with open('tree.json', 'r') as f:
tree = json.load(f)
reloc_change_dict = {}
nodes = {i: [] for i in range(8)}
for k in tree['nodes']:
nodes[int(k)] = [TreeNode.from_data(node_data) for node_data in tree['nodes'][k]]
# First find each leaf pairs
twins_leaf = reconstruct_twins_leaf(tree['leafs'])
# Then find the parent node of each pairs
for twin_leaf in twins_leaf:
find_twin_leaf_parent_node(twin_leaf, nodes[0], reloc_change_dict)
# Store which byte is modified by which level of the tree
levels_byte_index = {
0: 4,
1: 5,
2: 2,
3: 6,
4: 1,
5: 3,
6: 7,
}
# Then recover all remaining nodes, level by level
for n in range(6, -1, -1):
print(f'[*] Computing level {n}')
for twin_leaf in twins_leaf:
find_twin_leaf_nth_parent_node(
twin_leaf,
nodes[levels_byte_index[n]],
levels_byte_index[n],
8 - n,
reloc_change_dict
)
# Finally change nullsub_184() to the root node function
reloc_change_dict[0x463630] = twins_leaf[0][0].nth_parent_node(8).addr
Now that our reloc_change_dict is populated, all is left to do is to encode it into a valid input.
BASE_ADDR = 0x400000
def compute_reloc_inv_table(ght, alfheim_data):
letters = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
relocs = {}
for a in letters:
for b in letters:
for c in letters:
r = a + b + c
if (ord(a) + ord(b) + ord(c)) % 2:
new_func = ght.lookup(r)
if new_func is not None:
addr = int.from_bytes(
alfheim_data[
new_func - BASE_ADDR : new_func - BASE_ADDR + 8
],
"little",
)
relocs[addr] = r
return relocs
def encode_input(reloc_change_dict):
with open("alfheim", "rb") as f:
alfheim_data = f.read()
ght_data = alfheim_data[0x3B0:0x2C58]
# Exported with ida
with open("plt_got.bin", "rb") as f:
pltgot = f.read()
# Compute the reverse lookup table of the GNU hash table
# i.e. map symbol addr to YYY pattern
ght = GnuHashTable(ght_data)
reloc_inv_table = compute_reloc_inv_table(ght, alfheim_data)
# Store the JMPREL relocation table offsets of each symbols
jmprel_offset_for_addr = {}
for i in range(0, len(pltgot), 8):
addr = int.from_bytes(pltgot[i : i + 8], "little")
jmprel_offset_for_addr[addr] = i // 8
# Construct each (XXX-YYY) pairs
groups = []
for k in reloc_change_dict:
offset = jmprel_offset_for_addr[k]
new_func_addr = reloc_change_dict[k]
gnu_input_ht_for_new_func = reloc_inv_table[new_func_addr]
groups.append((offset, gnu_input_ht_for_new_func))
sorted_groups = sorted(groups, key=lambda x: x[0])
output = ""
for offset, name in sorted_groups:
output += hex(offset)[2:].zfill(3).upper() + "-" + name + ";"
return output
We are now done, and our script now display an input that we can give to the executable to get the final flag. Here are the IDA script used for extracting informations from the binary and the final solve script:
import json
from gnu_ht import GnuHashTable
from utils import *
BASE_ADDR = 0x400000
class TreeLeaf:
def __init__(self, addr, cst):
self.addr = addr # leaf function address
self.cst = cst # comparison constant
self.parent_node = None # parent node function
def nth_parent_node(self, n):
assert self.parent_node is not None
if n == 1:
return self.parent_node
else:
return self.parent_node.nth_parent_node(n - 1)
class TreeNode:
def __init__(self, addr, func1, func2, c1, c2):
self.addr = addr # node function address
self.func1 = func1 # func1 address
self.func2 = func2 # func2 address
self.c1 = c1 # func1 or constant
self.c2 = c2 # func2 or constant
self.parent_node = None # parent node function
@classmethod
def from_data(cls, data):
addr, (func1, c1), (func2, c2) = data
return cls(addr, func1, func2, c1, c2)
def nth_parent_node(self, n):
assert self.parent_node is not None
if n == 1:
return self.parent_node
else:
return self.parent_node.nth_parent_node(n - 1)
def reconstruct_twin_leaves(leafs_data):
twins = []
for i, (addr_leaf_1, d1) in enumerate(leafs_data):
for j, (addr_leaf_2, d2) in enumerate(leafs_data):
# j > i to avoid dubplicate (ie pairs (x, y) = (y, x))
if i != j and j > i:
d = get_num_bytes_differs(d1, d2)
if d == 1:
twins.append(
(TreeLeaf(addr_leaf_1, d1), TreeLeaf(addr_leaf_2, d2))
)
return twins
def find_twin_leaves_parent_node(
twin_leaves, possible_nodes, reloc_change_dict
):
valid_parent_nodes = 0 # should be equal to 1 at the end of the loop
leaf1, leaf2 = twin_leaves
for node in possible_nodes:
# At this stage the lsb byte of the input as not yet been
# "or"-ed with anything else, so it is still 0
x = 0
if node.c1 == (leaf1.cst & 0xFF) and node.c2 == (leaf2.cst & 0xFF):
reloc_change_dict[node.func1] = leaf1.addr
reloc_change_dict[node.func2] = leaf2.addr
leaf1.parent_node = node
leaf2.parent_node = node
valid_parent_nodes += 1
elif node.c1 == (leaf2.cst & 0xFF) and node.c2 == (leaf1.cst & 0xFF):
reloc_change_dict[node.func1] = leaf2.addr
reloc_change_dict[node.func2] = leaf1.addr
leaf1.parent_node = node
leaf2.parent_node = node
valid_parent_nodes += 1
if valid_parent_nodes == 0:
raise ValueError(
"Error, could not find a parent node function for twin leaves",
leaf1,
leaf2,
)
elif valid_parent_nodes != 1:
raise ValueError(
"Multiple parent node functions found for for twin leave",
leaf1,
leaf2,
)
def find_twin_leaves_nth_parent_node(
twin_leaves, possible_nodes, byte_index, n, reloc_change_dict
):
leaf1, leaf2 = twin_leaf
valid_nth_parent_nodes = 0
target_constant = leaf1.cst & (0xFF << (8 * byte_index))
for node in possible_nodes:
if node.c1 == target_constant:
sub_node = leaf1.nth_parent_node(n - 1)
reloc_change_dict[node.func1] = sub_node.addr
sub_node.parent_node = node
valid_nth_parent_nodes += 1
elif node.c2 == target_constant:
sub_node = leaf1.nth_parent_node(n - 1)
reloc_change_dict[node.func2] = sub_node.addr
sub_node.parent_node = node
valid_nth_parent_nodes += 1
if valid_nth_parent_nodes == 0:
raise ValueError(
f"Error, could not find the {n}-th parent node function for twin"
" leaves",
leaf1,
leaf2,
)
elif valid_nth_parent_nodes != 1:
raise ValueError(
f"Multiple {n}-th parent node functions found for for twin leaves",
leaf1,
leaf2,
)
def compute_reloc_inv_table(ght, alfheim_data):
letters = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
relocs = {}
for a in letters:
for b in letters:
for c in letters:
r = a + b + c
if (ord(a) + ord(b) + ord(c)) % 2:
new_func = ght.lookup(r)
if new_func is not None:
addr = int.from_bytes(
alfheim_data[
new_func - BASE_ADDR : new_func - BASE_ADDR + 8
],
"little",
)
relocs[addr] = r
return relocs
def encode_input(reloc_change_dict):
with open("alfheim", "rb") as f:
alfheim_data = f.read()
ght_data = alfheim_data[0x3B0:0x2C58]
# Exported with ida
with open("plt_got.bin", "rb") as f:
pltgot = f.read()
# Compute the reverse lookup table of the GNU hash table
# i.e. map symbol addr to YYY pattern
ght = GnuHashTable(ght_data)
reloc_inv_table = compute_reloc_inv_table(ght, alfheim_data)
# Store the JMPREL relocation table offsets of each symbols
jmprel_offset_for_addr = {}
for i in range(0, len(pltgot), 8):
addr = int.from_bytes(pltgot[i : i + 8], "little")
jmprel_offset_for_addr[addr] = i // 8
# Construct each (XXX-YYY) pairs
groups = []
for k in reloc_change_dict:
offset = jmprel_offset_for_addr[k]
new_func_addr = reloc_change_dict[k]
gnu_input_ht_for_new_func = reloc_inv_table[new_func_addr]
groups.append((offset, gnu_input_ht_for_new_func))
sorted_groups = sorted(groups, key=lambda x: x[0])
output = ""
for offset, name in sorted_groups:
output += hex(offset)[2:].zfill(3).upper() + "-" + name + ";"
return output
if __name__ == "__main__":
with open("tree.json", "r") as f:
tree = json.load(f)
reloc_change_dict = {}
nodes = {i: [] for i in range(8)}
for k in tree["nodes"]:
nodes[int(k)] = [
TreeNode.from_data(node_data) for node_data in tree["nodes"][k]
]
# First find each leaf pairs
twins_leaf = reconstruct_twin_leaves(tree["leafs"])
# Then find the parent node of each pairs
for twin_leaf in twins_leaf:
find_twin_leaves_parent_node(twin_leaf, nodes[0], reloc_change_dict)
# Store which byte is modified by which level of the tree
levels_byte_index = {
0: 4,
1: 5,
2: 2,
3: 6,
4: 1,
5: 3,
6: 7,
}
# Then recover all remaining nodes, level by level
for n in range(6, -1, -1):
print(f"[*] Computing level {n}")
for twin_leaf in twins_leaf:
find_twin_leaves_nth_parent_node(
twin_leaf,
nodes[levels_byte_index[n]],
levels_byte_index[n],
8 - n,
reloc_change_dict,
)
# Finally change nullsub_184() to the root node function
reloc_change_dict[0x463630] = twins_leaf[0][0].nth_parent_node(8).addr
encoded_relocs = encode_input(reloc_change_dict)
print(encoded_relocs)
import idautils
import ida_funcs
import ida_bytes
import ida_segment
import ida_ua
import json
def remove_upper_bytes(cst):
if cst == 0:
return 0
copy = 0
i = 0
while True:
copy |= (cst & 0xFF) << (8 * i)
if cst & 0xFF:
break
cst >>= 8
i += 1
return copy
def get_non_null_byte_idx(cst):
if cst == 0:
return None
i = 0
while cst:
cst >>= 8
i += 1
return i - 1
def extract_leaf_information(func, tree):
ea = func.start_ea
max_ea = func.end_ea
constant = None
has_cmp = False
has_setnz = False
while ea < max_ea:
insn = ida_ua.insn_t()
size = ida_ua.decode_insn(insn, ea)
if size == 0:
break
mnem = ida_ua.print_insn_mnem(ea)
if (
mnem == "mov"
and insn.Op1.type == ida_ua.o_reg
and insn.Op2.type == ida_ua.o_imm
):
if insn.Op1.reg == 0: # rax
constant = insn.Op2.value
elif mnem == "cmp":
has_cmp = True
elif mnem == "setnz":
has_setnz = True
ea += size
if constant is not None and has_cmp and has_setnz:
tree["leafs"].append((func.start_ea, constant))
else:
raise TypeError("Weird function at ", func.start_ea)
def extract_node_information(func, tree):
ea = func.start_ea
max_ea = func.end_ea
c1 = None
c2 = None
func1 = None
func2 = None
first_call_found = False
while ea < max_ea:
insn = ida_ua.insn_t()
size = ida_ua.decode_insn(insn, ea)
if size == 0:
break
mnem = ida_ua.print_insn_mnem(ea)
if (
mnem == "mov"
and insn.Op1.type == ida_ua.o_reg
and insn.Op2.type == ida_ua.o_imm
):
if insn.Op1.reg == 0: # rax
if first_call_found == False:
c1 = insn.Op2.value
else:
c2 = insn.Op2.value
elif (
mnem == "or"
and insn.Op1.type == ida_ua.o_reg
and insn.Op2.type == ida_ua.o_imm
):
if insn.Op1.reg in (0, 16): # rax, al
cst = insn.Op2.value
elif insn.Op1.reg == 20: # ah
cst = insn.Op2.value << 8
if first_call_found == False:
c1 = cst
else:
c2 = cst
elif mnem == "call":
if first_call_found == False:
func1_stub_addr = insn.Op1.addr
func1_call_insn = ida_ua.insn_t()
ida_ua.decode_insn(
func1_call_insn, func1_stub_addr + 4
) # +4 to ignore the endbr64
func1 = ida_bytes.get_qword(
func1_call_insn.Op1.addr
) # final address is in the got
first_call_found = True
else:
func2_stub_addr = insn.Op1.addr
func2_call_insn = ida_ua.insn_t()
ida_ua.decode_insn(
func2_call_insn, func2_stub_addr + 4
) # +4 to ignore the endbr64
func2 = ida_bytes.get_qword(
func2_call_insn.Op1.addr
) # final address is in the got
ea += size
# Sometimes one constant can be 0 and so it is not set in the assembly
assert c1 != None or c2 != None
assert func1 != None and func2 != None
if c1 == None:
c1 = 0
if c2 == None:
c2 = 0
# sometimes ida add 0xffff at the beginning of the constant
c1 = remove_upper_bytes(c1)
c2 = remove_upper_bytes(c2)
c1_idx = get_non_null_byte_idx(c1)
c2_idx = get_non_null_byte_idx(c2)
k = c1_idx if c1_idx else c2_idx # one might be None
tree["nodes"][k].append((func.start_ea, (func1, c1), (func2, c2)))
if __name__ == "__main__":
tree = {}
tree["leafs"] = []
tree["nodes"] = {i: [] for i in range(8)}
start_addr = 0x439EAB
end_addr = 0x44E1F0
for func_ea in idautils.Functions(start_addr, end_addr):
func = ida_funcs.get_func(func_ea)
if not func:
continue
# leaf function size is always 0x22
if func.end_ea - func.start_ea == 0x22:
extract_leaf_information(func, tree)
else:
extract_node_information(func, tree)
with open("tree.json", "w") as f:
f.write(json.dumps(tree, indent=4))
# then extract the .got.plt segment data
seg = ida_segment.get_segm_by_name(".got.plt")
data = idaapi.get_bytes(seg.start_ea, seg.end_ea - seg.start_ea)
with open("plt_got.bin", "wb") as f:
f.write(data[24:]) # skip the three first offsets
Flag: FCSC{7ba2672bdb2efc318c17683cace4079f203ff65c790dce0dfd313ea79d73a328}
Nessie
Un de vos amis quarantenaire a dépensé son insouciante jeunesse sur un jeu appelé Nessie. Il n’a jamais réussi à le finir malgré de longues heures passées devant sa NES.
Saurez-vous faire mieux que lui et obtenir sa reconnaissance éternelle ?
Le jeu a été testé avec succès sur les dernières versions de :
- Mesen,
- Nintendulator,
- puNES,
- fceux/fceumm (pour un meilleur rendu, dans les options vidéo, la zone de dessin doit être agrandie au maximum).
Musique : Neon Starlight - Necrophageon CC BY-SA 3.0 SFX : Tuï
Solves: 6
Difficulty: ⭐⭐⭐
This was the reverse challenge with the fewest solves, probably due to the exotic architecture. For this challenge, we are given a single file: nessie.nes. This is a NES game that can be emulated using the Mesen emulator. Running the game displays the following:

The goal of the game is to shoot a dinosaur that moves on a 2D map. The player has five auto-focus power-ups that allow them to lock the target directly onto the dinosaur’s position. After that, the player needs to manually move to the dinosaur’s position, which will change if the player is too slow. Up to this point, it’s not really clear what needs to be done to obtain a flag, so let’s dive into the game’s code.
The .nes format
According to the file utility, nessie.nes is a NES 2.0 ROM image
$ file nessie.nes
nessie.nes: NES ROM image (iNES) (NES 2.0): 68x16k PRG, 64x8k CHR [H-mirror] [NTSC]
According to the nesdev wiki, the NES 2.0 ROM format is as follows:
+----------------------------------------------------+
| Header (16 bytes) |
+----------------------------------------------------+
| Optional trainer area (512 bytes) |
+----------------------------------------------------+
| PRG-ROM area (N*16kib bytes) |
+----------------------------------------------------+
| CHR-ROM area (N'*8kib bytes) |
+----------------------------------------------------+
| Optional miscellaneous ROM area (rest of the file) |
+----------------------------------------------------+
The PRG-ROM area is where the game code lies. It is split into 16 KiB chunks called banks. The CHR-ROM is also split into 8 KiB chunks; this is where the game assets are stored. The header indicates how many banks are present in the ROM for the PRG and CHR areas, as well as whether there is an optional trainer area and an optional miscellaneous ROM area. In our case, the provided ROM contains only 8 PRG banks and 8 CHR banks (the file utility is incorrect on that part).
Loading the game into Ghidra
Unfortunately, there is no Ghidra loader for NES 2.0 ROMs. This means we will have to map everything manually. But before doing that, we need to understand how the NES actually handles ROMs. Each ROM specifies in its header a mapper ID. A mapper is a collection of circuits and hardware components embedded in a cartridge that extends the NES’s capabilities. For instance, it allows for additional RAM or saving the player’s progress on the cartridge. Another very important feature it provides is called bank switching.
The NES CPU, based on the 6502 processor, uses a 16-bit address space. This means it cannot support games larger than 64 KiB, which is a major limitation. To overcome this, the bank switching feature allows the system to dynamically swap code banks into memory at runtime, making it possible to support games larger than 64 KiB.
According to the header, our game uses mapper 1. The nesdev CPU memory map and mapper 1 pages tell us that with our header, the CPU memory mapping is as follows:
| Address range | Size | Purpose |
|---|---|---|
| $0000-$07FF | $0800 | Internal RAM |
| $0800–$1FFF | $1800 | 3x mirrored internal RAM |
| $2000–$2007 | $0008 | NES PPU registers |
| $2008–$3FFF | $1FF8 | 1023x mirrored PPU registers |
| $4000–$401F | $0020 | NES APU and I/O registers |
| $4020-$5FFF | $1FE0 | Unmapped |
| $6000-$7FFF | $2000 | Optional additional cartridge RAM (WRAM) |
| $8000-$BFFF | $4000 | 16 KiB PRG-ROM bank, switchable |
| $C000-$FFFF | $4000 | 16 KiB PRG-ROM bank, fixed to the last bank |
We can verify that this mapping is indeed correct with the Mesen debugger:

In our case, we can see that the switchable PRG bank mapped at $8000–$BFFF is the first bank (ID 0), and the one at $C000–$FFFF is indeed the last PRG bank (the eighth bank has ID 7). With that in mind, we can now extract the PRG banks from the .nes file and map everything into Ghidra. Since bank 7 references code from many banks, I decided to load the two banks separately to avoid confusing Ghidra. Here is the mapping used when reversing the code from $C000–$FFFF:

Reverse-engineering the game
According to nesdev, when the ROM starts, the CPU reads the address to start execution from the reset vector located at $FFFC–$FFFD. In our case, this address is $FFF1. This function is very similar to what is described on the nesdev init code page. Basically, it enables some CPU features, clears the RAM, and waits for the PPU (Picture Processing Unit) to be ready. Once everything is ready, it jumps to the game’s main code located at $80A7. Here is a simplified version of what the $80A7 function does:
void game_main(void)
{
byte bVar1;
show_start_screen_and_wait_start_press();
game_core_loop();
if (has_dino_ever_survived == 0) {
display_flag();
}
display_bad_hunter();
// Wait until start is pressed to restart the game
do {
bVar1 = read_input_ctrl_code();
} while ((bVar1 & 8) != 0);
reset_game();
}
If, after leaving the game core loop, the dinosaur never survived any rounds, meaning it got shot in time every time, then the flag is displayed on the game scene. Otherwise, a message stating “Bad hunter” is shown. Let’s look at this core loop.
void game_core_loop(void)
{
if (DAT_7fff != 0) {
/* player initial position */
player_x_position = 0x80;
player_y_position = 0x78;
/* Intial dino x, y position */
dino_x_position = 0x2;
dino_y_position = 0x40;
remaining_shots = 2000000;
rounds_left = 2000000;
FUN_FC72();
nlfsr_state = initial_nlfsr_state;
auto_focus_left = 5;
dino_state = 0;
update_scene();
wait_render();
tick_left_before_dino_state_change = 1;
dino_state = 6;
while( true ) {
key_press_event_code = read_input_ctrl_code();
if ((key_press_event_code & 8) != 0) {
on_start_pressed();
}
if ((key_press_event_code & 0x10) != 0) {
modify_player_position_up();
}
if ((key_press_event_code & 0x20) != 0) {
modify_player_position_down();
}
if ((key_press_event_code & 0x40) != 0) {
modify_player_position_left();
}
if ((key_press_event_code & 0x80) != 0) {
modify_player_position_right();
}
if ((key_press_event_code & 4) != 0) {
on_hide_gui_pressed();
}
if ((key_press_event_code & 2) != 0) {
on_auto_focus_pressed();
}
if ((key_press_event_code & 1) != 0) {
on_fire_key_pressed();
}
if ((bool)!update_game_state()) break;
update_scene();
wait_render();
}
update_scene();
return;
}
has_dino_ever_survived = has_dino_ever_survived + 1;
return;
}
The game core loop performs the following steps:
- Sets up the game’s global variables
- Calls the function
FUN_FC72() - Renders the game scene
- Reads the user input and updates the game state accordingly
- Stops when
update_game_state()returns 0
Exiting the game core loop will either display the flag or the “Bad hunter” message, so let’s take a look at the condition under which update_game_state() returns 0.
byte update_game_state(void)
{
byte new_pos_x;
byte new_pos_y;
if (dino_state != 0) {
if (dino_state == 1) {
tick_left_before_dino_state_change = tick_left_before_dino_state_change - 1;
if (tick_left_before_dino_state_change == 0) {
rounds_left = rounds_left - 1;
new_pos = nlfsr_gen_random();
dino_x_position = new_pos & 0xf8;
if (dino_x_position == 0) {
dino_x_position = 8;
}
if (dino_x_position == 0xf8) {
dino_x_position = dino_x_position -0x8;
}
new_pos_y = lfsr_gen_random();
dino_y_position = new_pos_y & 0xf8;
if (dino_y_position < 0x10) {
dino_y_position = dino_y_position + 0x10;
}
if (dino_y_position >= 0xE0) {
dino_y_position = dino_y_position & 0x7f;
}
tick_left_before_dino_state_change = nlfsr_gen_random();
if (0x4f >= tick_left_before_dino_state_change) {
tick_left_before_dino_state_change =
tick_left_before_dino_state_change + 0x50 +
(0x4f < tick_left_before_dino_state_change);
}
dino_state = 3;
}
}
else {
if (dino_state == 3) {
tick_left_before_dino_state_change = tick_left_before_dino_state_change - 1;
if (tick_left_before_dino_state_change == 0) {
has_dino_ever_survived = 1;
if (rounds_left == 0) {
dino_state = 0
return 0;
}
tick_left_before_dino_state_change = nlfsr_gen_random();
if (0x2f >= tick_left_before_dino_state_change) {
tick_left_before_dino_state_change =
tick_left_before_dino_state_change + 0x30 +
(0x2f < tick_left_before_dino_state_change);
}
dino_state = 1;
}
}
else {
if (dino_state != 6) {
dino_state = 0;
return 0;
}
tick_left_before_dino_state_change = tick_left_before_dino_state_change - 1;
if (tick_left_before_dino_state_change == 0) {
if (rounds_left == 0) {
dino_state = 0;
return 0;
}
tick_left_before_dino_state_change = nlfsr_gen_random();
if (0x2f >= tick_left_before_dino_state_change) {
tick_left_before_dino_state_change =
tick_left_before_dino_state_change + 0x30 +
(0x2f < tick_left_before_dino_state_change);
}
dino_state = 1;
/* Some more code that update the game scene similar to the code in update_scene() */
}
}
}
}
return dino_state;
}
The function is quite complex, so let’s break it down. The dino_state variable represents the current state of the dinosaur. Three values are possible:
| Value | Meaning |
|---|---|
| 1 | Invisible dinosaur. Occurs between two rounds, when the dinosaur moves to a new location. |
| 3 | Visible dinosaur. |
| 6 | Dead dinosaur. The dinosaur has been shot by the player. |
If the dinosaur is invisible and the timer tick_left_before_dino_state_change reaches zero, the dinosaur moves to a new position (based on a random number generator), becomes visible again, and the rounds_left counter is decremented.
On the other hand, if the dinosaur is in state 3 or 6 and the timer reaches zero, the dinosaur becomes invisible again, and the variable has_dino_ever_survived is set to 1 if the dinosaur is in state 3, except when there are no rounds left, in which case the function returns 0.
So, update_game_state returns 0 when there are no rounds left. Since rounds_left is initialized to 2,000,000 by the game core loop, in order to trigger display_flag, has_dino_ever_survived must remain equal to zero. This mean the dinosaur must not survive a single round, i.e., we must successfully shoot it 2,000,000 times in a row.
Obviously, playing the game manually is impossible given the number of rounds, so I chose to look at how the flag is generated.
Flag generation
To see what happens, I made the game jump to display_flag(). Here’s what we get:

After some testing, I noticed the flag changes with every shot fired, and appears to depend on multiple parameters related to the player’s position. So let’s examine the on_fire_key_pressed() function.
void on_fire_key_pressed(void)
{
// dino_state == 3 || dino_state == 6
if ((dino_state & 1) != 0) {
if (remaining_shots == 0) {
FUN_FC64(1,0);
return;
}
remaining_shots = remaining_shots - 1;
FUN_FC64(0,0);
FUN_FC8E(7,0xd,0);
if (((dino_state == 3) && (x_position == dino_x_position)) && (y_position == dino_y_position)) {
tick_left_before_dino_visibility_change = 0x5a;
dino_state = 6;
}
}
return;
}
This function appears to update the dinosaur’s state when shot and decreases the remaining shot count. However, it also calls two functions: FUN_FC64 and FUN_FC8E. The first one seems to handle a sound effect, but the second one is more mysterious. Looking at it in Ghidra, here’s what we see:
void FUN_FC8E(undefined param_1)
{
undefined uStack0000;
uStack0000 = param_1;
switch_bank(2);
FUN_8000(uStack0000);
reset_bank();
return;
}
This function works by first switching the PRG bank mapped at $8000-$BFFF to the third PRG bank of the .nes file. It then calls the new function located at $8000 with the three provided parameters (note that Ghidra’s decompilation is incorrect here). Finally, it switches back to the first PRG bank. Essentially, this function serves as a wrapper for the $8000 function of the third bank. Let’s examine it.
void FUN_8000(byte param_1,undefined param_2,undefined param_3)
{
byte ctr;
byte i;
player_info_addr = CONCAT11(param_3,param_2);
ctr = current_ctr;
n = param_1;
for (i = 0; i < n; i++) {
flag_hash_state[ctr] = *(byte *)(player_info_addr + (ushort)i);
ctr = ctr + 1;
if ((ctr & 0x3f) == 0) {
hash_round();
ctr = 0;
round_count = round_count + 1;
}
}
current_ctr = ctr;
return;
}
This function copies n bytes from the address specified by param_2 and param_3 into a buffer called flag_hash_state. Once 64 bytes have been copied in total, it triggers a hash_round function and resets the byte counter to 0, meaning next calls will overwrite the flag_hash_state buffer. Note that the address is passed as two arguments because the 6502 CPU uses 8-bit registers, requiring two registers to encode a 16-bit address.
The hash_round function appears to be a hashing function that processes the content of flag_hash_state and stores the result at $6063-$6082. Unfortunately, I couldn’t identify the hashing algorithm. Googling the constants used yielded no matches, meaning it might be either a custom hash function or a standard one with modified constants.
In summary, each shot triggers FUN_FC8E(7,0xD,0), which copies seven bytes starting from $000D into flag_hash_state. When the flag_hash_state buffer reaches 64 bytes, its content is hashed. Looking at the seven bytes stored at $000D with the Mesen memory debugger we figure out what they are:
| Address | Purpose |
|---|---|
| $000D | Player X position |
| $000E | Player Y position |
| $000F | has_dino_ever_survived |
| $0010-$0013 | rounds_left |
These values are hashed and stored at $6063-$6082. When the flag is displayed, here is what this memory area look like:
That’s our flag !!! This means the flag is simply the hash of data blocks containing these four variables, updated with each player shot.
Setting memory breakpoints at $6063-$6082 reveals two other functions besides the $8000 one that modify this area. The first is FUN_FC72(), called at the start of the game’s core loop. Like FUN_FC8E, it’s a wrapper around FUN_80BB() of the third bank. Here’s what it does:
void FUN_80bb(void)
{
byte i;
i = 31;
do {
flag_hash[i] = *(byte *)(i + 0x8908);
i = i - 1;
} while (-1 < (char)i);
current_ctr = 0;
round_count = 0;
return;
}
This function initializes the flag hash with a hardcoded byte array from $8908 and sets variables used by the $8000 function to zero.
Finally, the second function that modifies the flag hash is a wrapper around $8052 of the third bank. It is called in the display_flag function and seems to trigger hash_round to finalize the hashing process.
So the complete flag generation process is the following:
FUN_80bb: Initializes the flag hash with a hardcoded value at the beginning of the game core loop.FUN_8000: Updates the flag hash each time the player shoots. The flag is updated using: the player position, the value ofhas_dino_ever_survivedand the number of rounds left.FUN_8052: Computes the final flag hash.
Solving the challenge
My solution to the challenge was to replicate the flag generation process. Since reversing the hash_round function would be too complex, I chose to emulate it using the py65 emulator.
To obtain the correct final flag, we need to provide FUN_8000 with the exact player positions matching the dinosaur’s location for each shot. This requires reversing the nlfsr_gen_random() function that controls the dinosaur’s movement. Here’s its implementation:
byte nlfsr_gen_random(void)
{
byte bVar1;
bVar1 = nlfsr_state_1 >> 1 ^ nlfsr_state_1;
nlfsr_state_5 = bVar1 << 1 ^ bVar1;
nlfsr_state_1 = nlfsr_state_2;
nlfsr_state_2 = nlfsr_state_3;
nlfsr_state_3 = nlfsr_state_4;
nlfsr_state_4 = nlfsr_state_4 >> 3 ^ nlfsr_state_4 ^ nlfsr_state_5;
return nlfsr_state_4;
}
Rewriting this in Python gives us:
def get_next_random_value(random_state):
# some kind of nlfsr based on xor and bitshift
x = ((random_state[0] >> 1) ^ random_state[0]) & 0xff
random_state[4] = ((x << 1) ^ x) & 0xff
random_state[0] = random_state[1]
random_state[1] = random_state[2]
random_state[2] = random_state[3]
random_state[3] = ((random_state[3] >> 3) ^ random_state[3] ^ random_state[4]) & 0xff
return random_state[3]
Now that we have everything needed, we can simulate the complete flag generation process using this code:
import tqdm
from py65.devices.mpu6502 import MPU as MOS6502
class Nessie:
def __init__(self, prg_bank):
self.mpu = MOS6502()
# Empty RAM
initial_memory = [0x00] * 0x8000
# Map the PRG bank at $8000-$BFFF
initial_memory += prg_bank
# PRG mapped at $C000-$FFFF isn't used so we keep it empty
initial_memory += [0x00] * 0x4000
self.mpu.memory = initial_memory
self.random_state = [0, 0, 0, 0, 0]
def set_random_state(self, state):
self.random_state = state
def get_next_random_value(self):
x = ((self.random_state[0] >> 1) ^ self.random_state[0]) & 0xff
self.random_state[4] = ((x << 1) ^ x) & 0xff
self.random_state[0] = self.random_state[1]
self.random_state[1] = self.random_state[2]
self.random_state[2] = self.random_state[3]
self.random_state[3] = ((self.random_state[3] >> 3) ^ self.random_state[3] ^ self.random_state[4]) & 0xff
return self.random_state[3]
def get_next_dino_position(self):
x = self.get_next_random_value()
y = self.get_next_random_value()
x &= 0xF8
if x == 0:
x = 8
elif x == 0xF8:
x -= 0x8
y &= 0xF8
if y < 0x10:
y += 0x10
elif y >= 0xE0:
y &= 0x7F
# skip the next two values as they are used for dino state change delay
self.get_next_random_value()
self.get_next_random_value()
return x, y
def set_player_info(self, x, y, n):
self.mpu.memory[0xd] = x
self.mpu.memory[0xe] = y
self.mpu.memory[0xf] = 0 # has dino ever survived
self.mpu.memory[0x10] = n & 0xff
self.mpu.memory[0x11] = (n >> 8) & 0xff
self.mpu.memory[0x12] = (n >> 16) & 0xff
self.mpu.memory[0x13] = (n >> 24) & 0xff
def run_until(self, start, end):
self.mpu.pc = start
while self.mpu.pc != end:
self.mpu.step()
def init_flag_wram(self):
self.run_until(0x80bb, 0x80d4)
def update_flag_wram(self, ctr, addr):
# ctr is stored in A, addr in X and Y
self.mpu.a = ctr
self.mpu.x = addr & 0xff
self.mpu.y = (addr >> 8) & 0xff
self.run_until(0x8000, 0x8051)
def compute_final_flag(self):
self.run_until(0x8052, 0x80ba)
def get_flag_from_wram(self):
return bytes(self.mpu.memory[0x6063:0x6063+32]).hex()
if __name__ == '__main__':
with open('nessie.nes', 'rb') as f:
game_data = f.read()
third_bank = game_data[16+2*0x4000:16+3*0x4000]
nessie = Nessie(third_bank)
# nlfsr initial state before generating the first dino position
# found using the mesen memory debugger
nessie.set_random_state([
0x7B,
0x11,
0x85,
0x35,
0xA0
])
# call to FUN_80BB
nessie.init_flag_wram()
# call to FUN_8000 2_000_000 times with the right positions
n = 2_000_000
for i in tqdm.tqdm(range(n)):
x, y = nessie.get_next_dino_position()
nessie.set_player_info(x, y, n-i-1)
nessie.update_flag_wram(0x7, 0xD)
# call to FUN_8052
nessie.compute_final_flag()
print(f'FCSC{{{nessie.get_flag_from_wram()}}}')
After about an hour of runtime (yes, CPU emulation in pure Python is slow…), we successfully obtain the flag!
Flag: FCSC{2a178a4923c2303b85f99bbd5dcff4818d50ecf218c8e51d968a8eeab6e24f80}

